Тема. Застосування формул повної ймовірності та Байєса.

Практичне заняття.

Задача 1. В урні 3 білих і три чорних кулі. Із урни двічі навмання виймають по одній кулі, не повертаючи їх назад. Знайти ймовірність появи білої кулі при другому випробуванні (подія В), якщо при першому випробуванні витягли чорну кулю (подія А).

Розв’язання. Після першого випробування в урні лишилося 5 куль, серед яких 3 білих. Шукана умовна ймовірність Р_А(В) = 3/5.

Аналогічний результат можна отримати за формулою:

; .

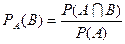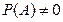Дійсно, ймовірність появи білої кулі при першому випробуванні Р(А)=3/6=1/2. Знайдемо ймовірність 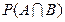того, що в першому випробуванні з’являється чорна куля, а в другому – біла. Загальна кількість виходів – сумісної появи двох куль, неважливо якого кольору, дорівнює кількості розміщень 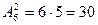. Із цієї кількості виходів події 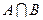сприяють 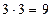виходів. Відповідно 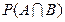= 9/30 = 3/10. Отже, шукана ймовірність:

= .

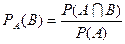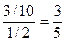Задача 2. За статистичними даними ремонтної майстерні в середньому на 20 зупинок токарного станка припадає: 10 – для заміни різця; 3 – через несправність приводу; 2 – через несвоєчасну подачу заготовок. Інші зупинки відбуваються через інші причини. Знайти ймовірність того, що зупинка відбулася через інші причини.

Розв’язання. Ймовірність того, що зупинка токарного станка відбулася для заміни різця, дорівнює: Р(А) = = 0,5. Ймовірність того, що зламався привід, дорівнює: Р(В) = 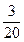= 0,15. Ймовірність того, що зупинка відбулася через несвоєчасну подачу заготовок: Р(С) = 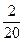= 0,1. Оскільки, Р(А), Р(В), Р(С) незалежні і утворюють повну групу подій з подією P(D) – зупинка відбулася через інші причини, то

Р(А) + Р(В) + Р(С) + P(D) = 1.

P(D) = 1 – Р(А) – Р(В) – Р(С),

P(D) = 1 – 0,5 – 0,15 – 0,1 = 0,25.

Задача 3. Вивчають результати екзамену з математики у двох групах. У першій групі є 30 студентів, з них 11 отримали відмінну оцінку, а в другій відповідно – 25 і 9. Яка ймовірність того, що навмання вибраний студент отримав на екзамені відмінну оцінку?

Розв’язання. Випробування полягає в тому, що ми навмання обираємо студента із двох груп. Позначимо через А подію, що навмання вибраний студент на екзамені отримав відмінну оцінку. Це може статися, коли студента вибрано із першої групи (відбулася подія В₁) або другої (В₂). Отже, Р(В₁)= 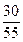, Р(В₂)= 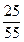. Використаємо формулу повної ймовірності:

Р(А)= .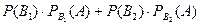

За умовою задачі , .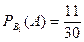

Звідси .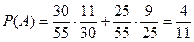

Задача 4. Два автомати виготовляють однакові деталі, які надходять на спільний конвеєр. Продуктивність першого автомата вдвічі більша за продуктивність другого. Перший автомат випускає в середньому 60% деталей без браку, а другий – 84%. Навмання взята з конвеєра деталь виявилась без браку. Знайти ймовірність того, що ця деталь виготовлена першим автоматом.

Розв’язання. Позначимо через А подію – деталь без браку. Можна сформулювати дві гіпотези: В₁ – деталь виготовлена першим автоматом (оскільки перший автомат виготовляє вдвічі більше деталей, ніж другий): Р(В₁)= 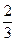; В₂ – деталь виготовлена другим автоматом, причому Р(В₂)= 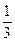. Умовна ймовірність того, що деталь буде без браку, якщо вона зроблена першим автоматом, дорівнює . Умовна ймовірність того, що деталь буде без браку, якщо вона зроблена другим автоматом, дорівнює . Ймовірність того, що навмання взята деталь виявиться без браку, за формулою повної ймовірності дорівнює:

Р(А) = .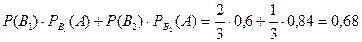

Шукана ймовірність того, що взята деталь без браку виготовлена першим автоматом, за формулою Байєса дорівнює:

Р_А(В₁) = .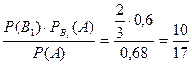

Задача 5. На двох верстатах-автоматах виробляють однакові деталі, які надходять на транспортер. Продуктивність першого верстата утричі більша, ніж другого, причому перший верстат виробляє нестандартну деталь з імовірністю 0,15, а другий — з імовірністю 0,2. Знайти ймовірність того, що навмання взята з транспортера деталь буде стандартною.

Розв’язання. Розглянемо події: — «деталь виготовлено на першому верстаті»; 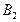— «деталь виготовлено на другому верстаті»; А — «вибрана деталь стандартна». Події 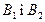несумісні й утворюють повну групу, що ж до події А, то вона може відбутись одночасно з кожною із цих подій. Умовні ймовірності настання події А відомі. Згідно з умовою, що продуктивність першого верстата утричі більша, ніж другого, знаходимо 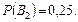За формулою повної ймовірності маємо: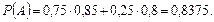

Задача 6. Партію виготовлених деталей перевіряли два контролери. Перший перевірив 45 %, а другий — 55 % деталей. Імовірність припуститися помилки під час перевірки для першого контролера становить 0,15, для другого — 0,1. Після додаткової перевірки в партії прийнятих деталей виявлено браковану. Оцінити ймовірність помилки для кожного контролера.

Розв’язання. Розглянемо події: — «деталь перевіряв перший контролер»; 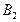— «деталь перевіряв другий контролер»; А — «виявлено браковану деталь». Події 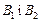несумісні й утворюють повну групу. Подія А відбулась одночасно з однією із цих подій, імовірності яких потрібно переоцінити. Застосуємо формулу Баєса.

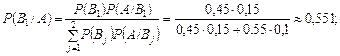
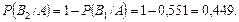
Отже, більш імовірно, що помилки припустився перший контролер.

Задача 7. Маємо дві партії однакових виробів. Перша складається з 15 стандартних і 4 нестандартних, друга — із 18 стандартних і 5 нестандартних виробів. Із навмання вибраної партії взято один виріб, який виявився стандартним. Знайти ймовірність того, що другий навмання взятий виріб також буде стандартним.

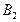Розв’язання. Розглянемо події: — «перший виріб взято з першої партії»; — «перший виріб узято з другої партії»; А — «перший узятий виріб стандартний»; С — «другий узятий виріб стандартний». За формулою повної ймовірності знаходимо ймовірність події А:

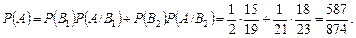
За формулою Баєса обчислюємо умовні ймовірност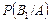і і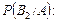

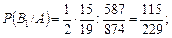
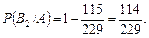
Імовірність події С знаходимо за формулою:

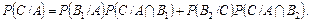
Умовні ймовірності такі: 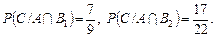Отже,

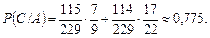
Задача 8. На двох верстатах-автоматах виробляють однакові деталі, які надходять на транспортер. Продуктивність першого верстата утричі більша, ніж другого, причому перший верстат виробляє нестандартну деталь з імовірністю 0,15, а другий — з імовірністю 0,2. Знайти ймовірність того, що навмання взята з транспортера деталь буде стандартною.

Розв’язання. Розглянемо події: — «деталь виготовлено на першому верстаті»; 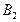— «деталь виготовлено на другому верстаті»; А — «вибрана деталь стандартна». Події 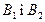несумісні й утворюють повну групу, що ж до події А, то вона може відбутись одночасно з кожною із цих подій. Умовні ймовірності настання події А відомі. Згідно з умовою, що продуктивність першого верстата утричі більша, ніж другого, знаходимо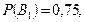 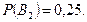За формулою повної ймовірності маємо: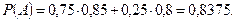

Задача 9. Партію виготовлених деталей перевіряли два контролери. Перший перевірив 45 %, а другий — 55 % деталей. Імовірність припуститися помилки під час перевірки для першого контролера становить 0,15, для другого — 0,1. Після додаткової перевірки в партії прийнятих деталей виявлено браковану. Оцінити ймовірність помилки для кожного контролера.

Розв’язання. Розглянемо події: — «деталь перевіряв перший контролер»; 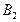— «деталь перевіряв другий контролер»; А — «виявлено браковану деталь». Події 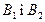несумісні й утворюють повну групу. Подія А відбулась одночасно з однією із цих подій, імовірності яких потрібно переоцінити. Застосуємо формулу Баєса.

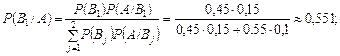
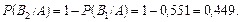
Отже, більш імовірно, що помилки припустився перший контролер.

Задача 10. Маємо дві партії однакових виробів. Перша складається з 15 стандартних і 4 нестандартних, друга — із 18 стандартних і 5 нестандартних виробів. Із навмання вибраної партії взято один виріб, який виявився стандартним. Знайти ймовірність того, що другий навмання взятий виріб також буде стандартним.

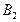Розв’язання. Розглянемо події: — «перший виріб взято з першої партії»; — «перший виріб узято з другої партії»; А — «перший узятий виріб стандартний»; С — «другий узятий виріб стандартний». За формулою повної ймовірності знаходимо ймовірність події А:

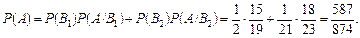
За формулою Баєса обчислюємо умовні ймовірност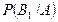і і

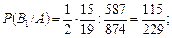
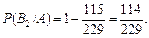
Імовірність події С знаходимо за формулою:

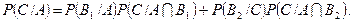
Умовні ймовірності такі: 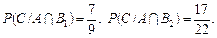Отже,

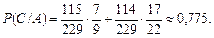
Задача 11. Вивчаються результати заліку з теорії ймовірностей у трьох групах. У першій групі є 30 студентів, з них 8 отримали відмінну оцінку, а в другій відповідно 28 і 6, в третій відповідно 32 і 8. Яка ймо­вірність, що навмання вибраний студент отримав на заліку відмінну оцінку?

Розв’язання. Позначимо через А подію, що навмання вибраний з трьох груп студент за результатами заліку з теорії ймовірностей отримав відмінну оцінку. Ця подія може відбутися тоді, коли студента вибрано з першої групи (відбулася подія В₁) або другої (В₂), або третьої (В₃). За статистичним означенням ймовірності .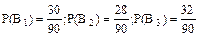

Використовуємо формулу повної ймовірності:

Р(А)= .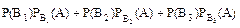

Якщо за умовою задачі:

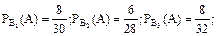то

Р(А) = .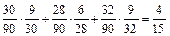

Задача 12. Дві економічні операції, що проводяться підприємцем одночасно для досягнення однієї загальної мети, мають ймовірність успіху, рівну р₁=0,8; p₂=0,6. Необхідно визначити ймовірність того, що досягнуто успіху в результаті першої операції.

Розв’язання. Нехай гіпотеза А₁ успіх першої економічної операції, Р(A₁)=0,8; гіпотеза А₂, успіх другої економічної операції, Р(A₂)=0,6.

Проведені економічні операції можуть дати результати:

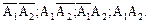
Відповідні ймовірності:

;

;

;

.

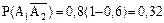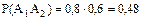Мета (подія С) буде досягнена в останніх трьох випадках, тому її ймовірність в першому випадку – 0, а в трьох останніх – 1.

Використовуючи формулу Байєса маємо:

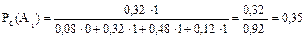
Дата добавления: 2015-08-17