Пропорционирование

Пропорционирование как метод количественного согласования частей и це­лого имеет в своей основе геометрическую или числовую закономерность, кото­рая способствует достижению эстетической целостности, гармоничности объем­но-пространственной формы за счет объединения ее размеров в какую-либо сис­тему.

Особенности пропорциональных систем тесно связаны со способами строи­тельства и измерения, которые применялись архитекторами той или иной эпохи. В древности пропорциональные системы получали путем относительно простых геометрических построений на основе треугольника, квадрата, прямоугольника или круга (рис.36).

В Древнем Египте широко использовалась система пропорционирования на основе «священного египетского треугольника» с соотношением сторон 3:4:5, по­зволяющего получать прямой угол со сторонами, выраженными в простых целых числах.

Система пропорционирования на основе вписанных квадратов давала гео­метрический ряд с отношением 1: √2, в котором чередовались иррациональные и целые числа (рис.36 (1)). Эта система использовалась как в Египте, так и в более позд­ние времена, например, в средневековье для построения готических башен. Так­же в период средневековья широко применялась система вписанных равносто­ронних треугольников.

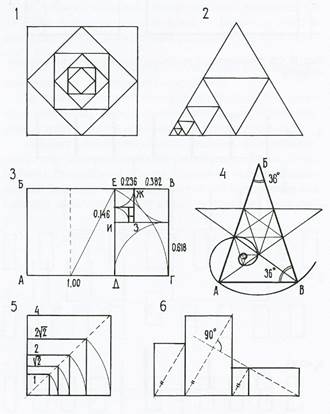Рис. 37 Системы пропорционирования на основе гномонических построений по принципу геометрического подобия: 1,2 – взаимовписанные квадраты и разносторонние треугольники; 3 – «свернутый» ряд прямоугольников «золотого сечения» (АБВГ, ГДЕВ, ЕЖЗИ. …); 4 – равнобедренный треугольник АБВ, в котором основание и сторона находятся в отношении «золотого сечения», на его основе строится пентаграмма; 5 – пропорции на основе соотношения стороны и диагонали квадрата 1: √2; 6 – принцип подобия прямоугольников на основе параллельности и перпендикулярности диагоналей.

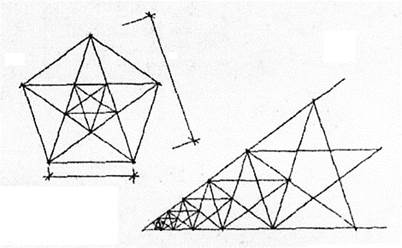
Рис. 38

Система пропорционирования на основе пентаграммы

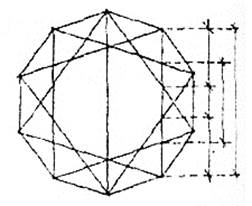
Рис. 39

Система пропорционирования на основе звездчатого десятиугольника

Перечисленные системы пропорционирования являются геометрическими, в числовом выражении они менее удобны в использовании, так как включают иррациональные числа. Однако существуют пропорциональные системы, основан­ные на числовых (арифметических) приемах согласования частей и целого; это так называемые модульные системы. Простейшим примером модульной системы является масштабная сетка, в которую вписываются как общий абрис, так и дета­ли сооружения. Модульная система пропорционирования предполагает существование модуля - условной единицы измерения. Применяемая нашей стране мо­дульная система (ЕМС) так же использует единый модуль (М = 100 см) на основе которого путем его членения или умножения получают все принятые в строитель­стве размеры.

Пропорционирование может быть использовано в двух основных направле­ниях: как метод создания целостной формы и как метод выявления закономерно­стей построения уже созданных архитектурных форм. При этом следует понимать, что закономерности, выявленные в уже созданных архитектурных формах, далеко не всегда осознанно применялись их создателями.

Пропорционирование - достаточно сильное, но далеко не единствен­ное средство гармонизации архитектурной формы и поэтому одно только совершенство пропорции еще не является гарантом получения совершен­ного архитектурного произведения.

Дата добавления: 2015-08-17