Читайте также:
|
В теории и практике архитектуры хорошо известны такие виды закономерных (однородных) изменений величин, как арифметическая гармоническая и геометрическая прогрессии.
Арифметическая прогрессия выражается рядом чисел, в котором каждое
последующее число больше предыдущего на одну и ту же величину. Простейшим примером арифметической прогрессии является ряд натуральных чисел 0, 1,2, 3, 4, 5 и т.д.
Гармоническая прогрессия - это ряд чисел обратных ряду чисел арифметической прогрессии, например: 1/2, 1/3, 1/4, 1/5, 1/6, 1/7. Отношения между соседними членами гармонического ряда по мере его возрастания так же, как и в арифметической прогрессии, изменяются от контрастных к нюансным.
Геометрическая прогрессия представляет собой ряд чисел, в котором каждое последующее число больше (или меньше) предыдущего в одно и то же число
раз. Например: 1,2,4,8,16,...: 1, 1/2, 1/4, 1/8, 1/16.
Широко используются в архитектуре аддитивные ряды, построенные на суммировании чисел. Например, в ряде чисел 1, 2, 3, 5, 8, 13, 21, 34,...(ряд Фибоначчи) каждый последующий член, начиная с 3-го равен сумме двух предыдущих. Отношение между смежными членами такого ряда, начиная с 5-го члена, практически постоянно и равно 1,62.
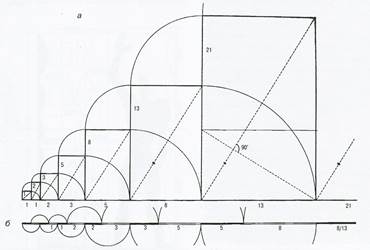Рис. 34 Линейная и двухмерная интерпретация ряда Фибоначчи: а – двухмерная – прямоугольники, начиная с 8:13, 13:21, приобретают пропорции «золотого сечения» и взаимное подобие – их диагонали параллельны и взаимоперпендикулярны; б – линейная - стабилизация пропорций «золотого сечения», начиная от 3:5:8; 5:8:13…
Дата добавления: 2015-08-17; просмотров: 348 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Понятие о пропорции в архитектуре | | | Понятие золотого сечения |