Перигелий

Афелий

(от греческих слов άπ ò — от и ηλίον — солнце) — та точка орбиты какого-нибудь светила, движущегося около Солнца, которая дальше всего отстоит от Солнца. Эта точка лежит поэтому на конце оси того эллипса, который описывается планетой, кометой или иными светилами около Солнца. В параболической орбите, где ось имеет бесконечную длину, об афелии, в собственном смысле, не может быть речи, однако здесь под направлением А. подразумевают направление оси парболы, противоположное направлению к перигелию, т. е. к вершине ее. В А. скорость всякой планеты наименьшая, в противоположной точке, в перигелии, наибольшая. Различие в расстоянии от Солнца в этих двух точках и зависящее от этого различие в скоростях находится в прямой связи с эксцентриситетом орбиты светила. Вследствие незначительности эксцентриситета всех планетных орбит, афелий и перигелий их отстоят от Солнца на расстояниях, мало отличающихся одно от другого, и скорости планет в этих точках также мало различаются. Обратное имеет место для комет, орбиты которых сильно эксцентричны. Так, например, комета 1680 г. движется в перигелии со скоростью в 137000 раз большей, чем в афелии, между тем как, например, наша Земля движется в афелии со скоростью, которая только на 0,03 отличается от скорости ее в перигелии. Точки А. и перигелия, вместе взятые, называются апсидами.

Перигелий

(от пери... и греч. helios - Солнце), ближайшая к Солнцу точка орбиты небесного тела, движущегося вокруг Солнца по одному из конических сечений - эллипсу, параболе или гиперболе. Вследствие действия возмущающих сил планет происходит изменение положения перигелия в пространстве. У ближайшей к Солнцу планеты - Меркурия обнаружено перемещение перигелия, происходящее в соответствии с уточнённым законом тяготения, следующим из общей теории относительности. Расстояние перигелия от центра Солнца называется перигелийным расстоянием.

Третий закон Кеплера. Квадраты периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.

Современная формулировка первого закона дополнена так: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола. В отличие от двух первых, третий закон Кеплера применим только к эллиптическим орбитам. Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения. Для определения масс небесных тел важное значение имеет обобщение Ньютоном третьего закона Кеплера на любые системы обращающихся тел.

Третий закон Кеплера. Скорости близких к Солнцу планет значительно больше, чем скорости далеких. Пояснение к рисунку справа - Скорости близких к Солнцу планет значительно больше, чем скорости далеких. В обобщенном виде этот закон обычно формулируется так: квадраты периодов T1 и T2 обращения двух тел вокруг Солнца, помноженные на сумму масс каждого тела (соответственно M1 и M2) и Солнца (М), относятся как кубы больших полуосей a1 и a2 их орбит: При этом взаимодействие между телами M1 и M2 не учитывается. Если пренебречь массами этих тел в сравнении с массой Солнца (т.е. M1 << М, M2 << М), то получится формулировка третьего закона, данная самим Кеплером:

Третий закон Кеплера можно использовать, чтобы определить массу двойных звезд.

Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов F1 и F2) есть величина постоянная и равная длине большой оси: r1 + r2 = |AA´| = 2a. Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет е = ОF/OA. При совпадении фокусов с центром е = 0, и эллипс превращается в окружность. Большая полуось а является средним расстоянием от фокуса (планеты от Солнца): a = (AF1 + F1A')/2. Так как при движении по эллипсу полная энергия отрицательна, большая полуось больше нуля. Длина малой полуоси b зависит от секториальной скорости тела (т.е. скорости изменения площади, заметаемой радиус-вектором). Круговые орбиты являются вырожденным случаем эллиптических. Записывая второй закон Ньютона, получим, что кинетическая и потенциальная энергия тела на круговой орбите связаны соотношением: 2K = –U. Применяя закон сохранения энергии, легко получить, что K = –E. Т.о. при круговом движении сумма полной и кинетической энергии всегда равна нулю. Элементы орбиты характеризуют форму, размеры и ориентацию в пространстве орбиты небесного тела, а также положение тела на этой орбите. В настоящее время для описания положения планеты или спутника широко используются оскуллирующие элементы.

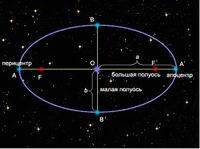
Важнейшие точки и линии эллипса.

Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов F1 и F2) есть величина постоянная и равная длине большой оси: r1 + r2 = |AA´| = 2a. Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет е = ОF/OA. При совпадении фокусов с центром е = 0, и эллипс превращается в окружность. Большая полуось а является средним расстоянием от фокуса (планеты от Солнца): a = (AF1 + F1A')/2.

Полная формулировка законов движения космических тел в центральном поле тяготения и определение понятий, связанных с описанием движения космических тел и характеристиками орбит:

Основные характеристики движения космического тела в пределах Солнечной системы – называются элементами орбиты и определяются относительно плоскости эклиптики рисунок слева.

Угол i между плоскостью орбиты и эклиптикой называется ее наклонением: при 0њ £ i < 90њ космическое тело движется вокруг Солнца в прямом направлении (как Земля); при 90њ £ i < 180њ – в обратном направлении.

Точки, в которых орбита космического тела пересекается с плоскостью эклиптики, называются узлами егоорбиты: восходящим узлом в направлении северного полюса эклиптики и нисходящим узлом в направлении южного полюса эклиптики.

Угол b между центром Солнца, восходящим узлом орбиты и точкой весеннего равноденствия называется гелиоцентрической долготой восходящего узла и вместе с наклонением определяет пространственное положение плоскости орбиты космического тела.

Угол w между центром Солнца, восходящим узлом орбиты и точку перигелия называется угловым расстоянием перигелия от узла, отсчитывается в плоскости орбиты в направлении движения космического тела и определяет положение орбиты в ее плоскости.

МОУ лицей

Тема: «Законы Кеплера»

Петров Владислав Игоревич (1997)

Андреева Александра (199)

@mail:

Телефон:

Дата добавления: 2015-08-17