Физика Твердого Тела

К физическим свойствам твердых тел относятся механические, тепловые, электрические, магнитные и оптические свойства. Их изучают, наблюдая, как ведет себя образец при изменении температуры, давления или объема, в условиях механических напряжений, электрических и магнитных полей, температурных градиентов, а также под воздействием различных излучений - света, рентгеновских лучей, пучков электронов, нейтронов и т.п. Значительная часть лабораторного оборудования, необходимая для изучения этих свойств, сама состоит из твердотельных устройств. Химические свойства твердых тел особенно существенны при изучении поверхностных явлений.

C имметрия и классификация кристаллов. Кристаллографией (в несколько ограниченном смысле слова) называется наука, описывающая геометрические свойства кристаллов и их классификацию на основе понятия симметрии. Изучение кристаллической структуры лежит в основе физики твердого тела. Основная сумма данных кристаллографии была накоплена уже к концу 19 в.

Образцы природных минералов, например берилла, алмаза или каменной соли, имеют плоские грани и прямые ребра, определяющие их типичный внешний вид. Такие вещества принято называть кристаллами, хотя еще до конца средних веков этот термин применялся исключительно к кварцу. Первые минералоги интересовались прежде всего именно формой кристаллов, т.е. их морфологией. Н.Стенон, датский лекарь при дворе великого герцога Тосканы и исследователь в области геологии, в 1669 открыл закон постоянства углов между гранями. Согласно закону Стенона, углы между соответствующими гранями кристалла данного вещества одни и те же для всех его кристаллов. Справедливость этого закона была многократно подтверждена, в особенности после многочисленных измерений, проведенных Р.де Лилем в 1772. Задолго до этого такие ученые, как Кеплер, Декарт, Гюйгенс и Гук, высказывали предположения о том, что внешние формы кристаллов отражают правильное (регулярное) внутреннее расположение сферических или эллипсоидальных частиц. В 1782 Р. Аюи обобщил эти представления. Он считал, что трехмерный кристалл, имеющий форму параллелепипеда, состоит из одинаковых "кирпичиков". Исходя из такого представления, Х.Вейсс в 1808 ввел систему кристаллографических осей, определяемую тремя векторами a, b, c, которые соответствуют трем сторонам "кирпичика" Аюи, т.е. элементарной ячейки. Бесконечное множество точек (узлов), положение которых определяется вектором R = n₁a + n₂b + n₃c, где n₁, n₂ и n₃ – целые числа, называется пространственной решеткой. Такая решетка - не кристалл, а чисто математический объект. Однако с ее помощью можно построить кристалл, если в каждый ее узел поместить повторяющийся элемент, состоящий из одного или нескольких атомов (рис. 2). И наоборот, можно построить пространственную решетку, соответствующую кристаллу, если выбрать произвольную точку (узел) P₁, а затем найти все остальные точки P₂, P₃,..., обладающие тем свойством, что окружение этих точек выглядит во всех отношениях в точности так же, как оно выглядит из точки P₁. Множество точек P₁, P₂, P₃,... в таком случае образует пространственную решетку кристалла. Классификация решеток и кристаллов на основе понятия симметрии требует строгих определений. Операцией симметрии называется такая операция, которая, будучи произведена над твердым телом, оставляет это тело неизменным, и тогда это тело называется инвариантным относительно этой операции. (Например, сфера инвариантна по отношению к вращению вокруг любой оси, перемещению из одного места в другое, отражению в зеркале и т.п.) Если двумерную решетку на рис. 2 подвергнуть перемещению, задаваемому вектором a, то мы вновь получим исходную решетку; то же справедливо, разумеется, и по отношению к перемещению, задаваемому вектором b. Вообще говоря, решетка с элементарной ячейкой, заданной тремя векторами a, b, c, инвариантна относительно всех операций трансляции (переноса), определяемых равенством T = n₁a + n₂b = n₃c, где n₁, n₂, n₃ - целые числа. Совокупность всех таких операций называется трансляционной группой данной решетки.

Рис. 2. КРИСТАЛЛ можно построить, поместив в каждую точку пространственной решетки атом или группу атомов.

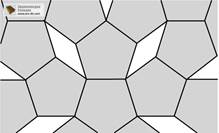
Рис. 3. ПЯТИУГОЛЬНИКИ не могут заполнить всю плоскость.

Существуют и другие операции симметрии для пространственной решетки, а именно те, при которых данная точка остается фиксированной (неподвижной). Подобные операции называются точечными и включают в себя вращения вокруг осей, проходящих через данную точку, а также зеркальные отражения в плоскостях, проходящих через данную точку. В случае двумерной решетки, изображенной на рис. 2, можно представить себе, например, ось, проходящую через какую-либо точку решетки перпендикулярно плоскости рисунка. Поворот вокруг этой оси на 180° не меняет решетку. Принято говорить, что такая ось обладает симметрией 2-го порядка. В общем случае тело обладает осью симметрии n-го порядка, если поворот тела на угол (360°b/n) оставляет тело неизменным. Например, каждая пространственная диагональ куба является для него осью симметрии 3-го порядка, а ось, проведенная через центр куба перпендикулярно какой-либо паре его граней, является осью симметрии 4-го порядка. Полный набор операций симметрии, возможных при условии неподвижности данной точки и оставляющих тело неизменным, называется точечной группой этого тела. Для пространственной решетки или кристалла точечная симметрия ограничена требованием выполнения также трансляционной симметрии. Это сокращает число возможных осей вращения до четырех, обладающих соответственно симметрией 2-, 3-, 4- и 6-го порядков. Рис. 3 поясняет, почему, например, решетка не может обладать осью симметрии 5-го порядка: плоскость нельзя покрыть пятиугольниками.

Существует лишь семь различных точечных групп для пространственных решеток; ими определяются семь кристаллических систем, или сингоний. Каждая сингония может быть охарактеризована видом элементарной ячейки, т.е. углами α, b, g между осями a, b, c и соотношением длин этих осей. Классификация соответствующих типов элементарных ячеек и наименования соответствующих кристаллических сингоний приведены ниже; обозначения ребер и углов ячеек соответствуют рис. 4.

Рис. 4. ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА, основной "кирпичик" кристалла.

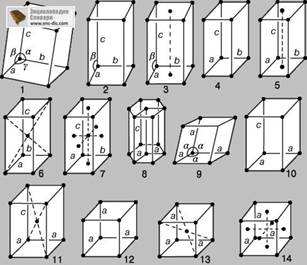  Рис. 5. ЭЛЕМЕНТАРНЫЕ ЯЧЕЙКИ всех 14 основных видов.

Полная группа симметрии, или пространственная группа кристалла, является совокупностью всех операций симметрии (точечных операций, трансляций, а также их всевозможных комбинаций), по отношению к которым решетка инвариантна. Существует 14 различных пространственных групп, которыми может обладать решетка; им соответствуют 14 различных пространственных решеток (рис. 5). Впервые эти решетки были описаны Браве в 1848 на основе тщательного геометрического анализа и носят его имя. (Каждая решетка Браве принадлежит к одной из семи кристаллических сингоний.)

Дата добавления: 2015-08-20