
|
Читайте также: |
Собственная частота крутильных колебаний расщепленной фазы (РФ), как и одиночного провода используется при решении многих прикладных задач, например при исследовании пляски ВЛ, при расчете параметров некоторых типов гасителей пляски проводов и.т.д. Как известно, оценка частоты может быть выполнена аналитическим способом. Однако, в этом случае возникает необходимость обоснования адекватности расчетной формулы. Адекватность расчетной формулы может быть проверена путем сопоставления теоретической и экспериментальной частоты. В случае существенного расхождения следует учитывать при выводе расчетных формул тех факторов, которые были отброшены с целью упрощенияматематических соотношений.
В статье, при выводе расчетной формулы для определения теоретической частоты не учитывается кривизна провисания провода в пролете. Анализируются соответствия между теоретическими и экспериментальными частотами свободных крутильных колебаний расщепленной фазы ЛЭП. По результатам сопоставления делается соответствующие выводы.
Ключевые слова: линия электропередачи, пляска проводов, расщепленная фаза, частота крутильного колебания, экспериментальная частота.
Экспериментальная частота крутильных колебаний РФ.
Одной из задач анализа является оценка соответствия между теоретической и экспериментальной частотой свободных крутильных колебаний расщепленной фазы (РФ) высоковольтных ЛЭП. Существенные расхождения в этом случае могут привести к заметным ошибкам при расчете параметров пляски проводов.
Для решения сформулированной задачи была проведена серия экспериментов на опытном полигоне КазНИИЭ им. акад. Ш.Ч. Чокина, при которых измерялась собственная крутильная частота РФ. Опыты проводились в безветренную погоду, с проводами различных марок при широком диапазоне изменения натяжения. Варьировались также число полуволн и длина пролета и число расщепления фазы.
Экспериментальная оценка крутильных частот РФ осуществлялось следующим образом: фиксировались секундомером время, необходимое для совершения РФ нескольких циклов колебаний (обычно 10 полных колебаний). Крутильная частота определялось путем деления число колебаний на фиксированное время. Начальное натяжение провода в процессе эксперимента фиксировались динамометром. При обработке опытных данных использованы вместо начального натяжения  (даН) механическое напряжение
(даН) механическое напряжение  (даН /мм2 ).
(даН /мм2 ).
Экспериментальные данные по частотным характеристикам проводов высоковольтных ВЛ приведены на рисунках 1 – 4, 8.
На рисунках построены зависимость частоты от начального напряжения и число полуволн по экспериментальным данным (точечные изображения), а также построены аппроксимирующие теоретические кривые (сплошные кривые). Аппроксимирующие кривые вычислен по формуле, известные из области теорий колебаний струны /1 /.

Рисунок 1. Сопоставления экспериментальной и теоретической частоты при различных напряжениях. Исходные данные:  ,
,  ,
,  . Сплошные кривые - теоретические данные, точечные изображения – экспериментальные данные.
. Сплошные кривые - теоретические данные, точечные изображения – экспериментальные данные.

Рисунок 2. Сопоставления экспериментальной и теоретической частоты при различных напряжениях. Исходные данные:  ,
,  ,
,  . Сплошные кривые - теоретические данные, точечные изображения – экспериментальные данные.
. Сплошные кривые - теоретические данные, точечные изображения – экспериментальные данные.
Таблица Частота крутильного колебания расщепленной фазы.
 , даН/мм2 , даН/мм2
| Число полуволн

| Число полуволн 
| Число полуволн 
| Число полуволн 
| Число полуволн

| |
 , рад/сек , рад/сек
|  , рад/сек , рад/сек
|  , рад/сек , рад/сек
|  ,рад/сек ,рад/сек
|  , рад/сек , рад/сек
| ||
ℓ = 288 м. АС-300 /39.
Число расщепления n = 5 шт. Число распорок в пролете 5 шт.
Амплитуда крутильного колебания  150 - 200 150 - 200
| ||||||
| 4,5 |  0,45 0,45
| 0,42 | 0,6 | |||
| 5,4 | 0,38 | 0,43 | 0,63 | 0,83 | 1,0 | |
| 6,6 | 0,36 | 0,47 | 0,69 | 0,92 | 1,19 | |
| 8,1 | 0,35 | 0,54 | 0,77 | 1,0 | 1,25 | |
| 8,8 | 0,34 | 0,79 | ||||
| 11,4 | 0,37 | 0,63 | 0,89 | 1,25 | 1,45 | |
| 12,4 | 0,38 | 0,66 | 0,93 | 1,27 | 1,52 | |
| 13,1 | 0,38 | 0,66 | 0,98 | 1,35 | 1,61 | |
ℓ = 354 м. АС -300 / 39
Число расщепления n = 8 шт. Число распорок в пролете 7 шт.
Амплитуда крутильного колебания  150 - 200 150 - 200
| ||||||
| 5,7 | 0,33 | 0,37 | 0,55 | 0,72 | 0,89 | |
| 7,2 | 0,29 | 0,41 | 0,59 | 0,78 | 1,0 | |
| 7,6 | 0,29 | 0,41 | 0,63 | 0,82 | 1,02 | |
| 8,8 | 0,29 | 0,45 | 0,67 | 0,89 | 1,11 | |
Таблица.... Характеристики проводов ЛЭП
| Марка | Диаметр
 , мм , мм
| Сечение
 , мм2 , мм2
| Модуль упругости
 , Дан/мм2 , Дан/мм2
| Вес 1 м провода
 , Дан/м , Дан/м
| Примечание (старое название) |
| АС- 50/8 | 9,6 | 56,3 | 0,196 | АС-50 | |
| АС- 70/11 | 11,4 | 79,3 | 0,275 | АС- 70 | |
| АС- 95/16 | 13,5 | 111,3 | 0,386 | АС- 95 | |
| АС- 120 | 15,2 | 0,492 | |||
| АС- 150 | 174,6 | 0,617 | |||
| АС- 185 | 215,4 | 0,771 | |||
| АС- 240/32 | 21,6 | 275,7 | 0,921 | АСО- 240 | |
| АС- 300 | 24,2 | 351,3 | 1,257 | ||
| АС- 300/39 | 339,6 | 1,132 | |||
| АС- 330/43 | 25,2 | 1,255 | |||
| АС- 400 | 27,2 | 441,5 | 1,5 | ||
| АС- 400/51 | 27,5 | 1,49 | |||
| АС- 600/72 | 33,2 | 650,2 | АСО- 600 |
Вывод расчетной формулы для определения крутильной частоты РФ.
Крутильная частота колебаний, как одиночного провода, так и расщепленной фазы зависит от крутильной жесткости. Крутильная жесткость может быть определена, если между крутящим моментом и углом закручивания фазы установлены функциональные зависимости. Ниже установлены зависимости между крутящим моментом, приложенным к расщепленной фазе и углом закручивания фазы. При выводе зависимости пренебрегаем кривизной провисания провода в пролете.
Под воздействием приложенного крутящего момента расщепленная фаза закручивается на некоторый угол  . Если провода не имеют начального провисания, то все провода расщепленной фазы создают одинаковые по величине сопротивления внешнему крутящему моменту (возвращающий момент). Поэтому, достаточно определить величину возвращающего момента для одного провода и результат увеличить пропорционально числу проводов в фазе. При выводе пренебрегаем дополнительным моментом, возникающим от поворота отдельных нитей вокруг собственной оси. Расчетная схема приведена на рисунке 1.
. Если провода не имеют начального провисания, то все провода расщепленной фазы создают одинаковые по величине сопротивления внешнему крутящему моменту (возвращающий момент). Поэтому, достаточно определить величину возвращающего момента для одного провода и результат увеличить пропорционально числу проводов в фазе. При выводе пренебрегаем дополнительным моментом, возникающим от поворота отдельных нитей вокруг собственной оси. Расчетная схема приведена на рисунке 1.
Для сохранения геометрии расщепленной фазы, между проводами вдоль пролета устанавливают распорки. Длина одного подпролета  (расстояние между распорками) определяется по формуле
(расстояние между распорками) определяется по формуле
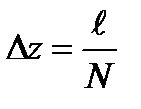 (1)
(1)
где  - длина пролета,
- длина пролета, 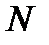 - число подпролетов в пролете (
- число подпролетов в пролете ( )
)
Радиус расщепления фазы  определяется, если известна расстояния между соседними проводами расщепленной фазы
определяется, если известна расстояния между соседними проводами расщепленной фазы  .
.
 (2)
(2)
где  число проводов в фазе (число расщепления).
число проводов в фазе (число расщепления).
Если крутящий момент приложен в середине пролета, то величина момента определяется по формуле (рисунок 1б)
 (3)
(3)
где  - результирующая возвращающая сила одиночного провода,
- результирующая возвращающая сила одиночного провода,  - плечо этой силы.
- плечо этой силы.
Из рисунка 1 следует




где  угол наклона подпролета,
угол наклона подпролета,  относительное перемещение смежных распорок,
относительное перемещение смежных распорок,  угол закручивания распорки в пределах одного подпролета,
угол закручивания распорки в пределах одного подпролета,  натяжение провода, соответствующее закрученному состоянию.
натяжение провода, соответствующее закрученному состоянию.
Выразим угол  через угол поворота фазы в середине пролета
через угол поворота фазы в середине пролета 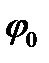

Подставляя установленные зависимости в основное уравнение (3), преобразуя, находим
 (4)
(4)
Выражение (4) устанавливает функциональную зависимость между крутящим моментом и углом закручивания расщепленной фазы.
Следует отметить, что при закручиваний фазы увеличивается натяжения провода. Если между натяжением и деформацией существует линейная зависимость, то согласно закону Гука
 (5)
(5)
где  длина закрученного провода,
длина закрученного провода,  начальное натяжение,
начальное натяжение,  натяжение закрученного провода, Е – модуль упругости,
натяжение закрученного провода, Е – модуль упругости,  площадь поперечного сечения провода.
площадь поперечного сечения провода.
Разность длин проводов
 (6)
(6)
Решив уравнения (5) и (6), находим искомое натяжение
 (7)
(7)
Если известна зависимость (4), то крутильная жесткость фазы может быть определена известной формулой /1/
 (8)
(8)
При практических расчетах можно принять  , поскольку для полномасштабных ВЛ
, поскольку для полномасштабных ВЛ

Кроме того, для небольших амплитуд крутильных колебаний  (что соответствует условиям эксперимента) можно положить
(что соответствует условиям эксперимента) можно положить

С учетом последнего, выражение для крутильной жесткости РФ преобразуется к виду
 (9)
(9)
Если известна крутильная жесткость РФ, то крутильная частота определяется по известной формуле /2/
 (10)
(10)
где JРФ– момент инерции РФ, определяется по формуле
 (11)
(11)
ЛИТЕРАТУРА
1 Бекметьев Р.М., Жакаев А.Ш., Ширинских Н.В. Пляска проводов воздушных линий электропередачи.- изд. «Наука» КазССР, Алма-ата, 1979
2 Светлицкий В.А., Стасенко И.В. Сборник задач по теории колебаний – М.: «Высшая школа», 1973.
Таблица 1 Зависимость угла закручивания расщепленной фазы  от приложенного крутящего момента Мкр. Крутящий момент приложен в середине пролета. Диаметр диска – 0,615 м. (провод АС-300/39, длина анкерного пролета
от приложенного крутящего момента Мкр. Крутящий момент приложен в середине пролета. Диаметр диска – 0,615 м. (провод АС-300/39, длина анкерного пролета  м, число расщепления
м, число расщепления  шт.)
шт.)
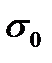 ,
даН/мм2 ,
даН/мм2
| Ргр, даН | Мкр,
даН  м м
| Число распорок
в пролете 
| Число распорок
в пролете 
| Число распорок
в пролете 
| |||
 , м , м
| 
|  , м , м
| 
|  , м , м
|  , ,
| |||

| 00 | 00 | ||||||
| 19,8 | 12,2 | 0,03 | 6,10 | |||||
| 45,4 | 28,0 | 0,07 | 13,70 | |||||
| 71,4 | 44,0 | 0,12 | 22,50 | |||||
| 96,4 | 59,3 | 0,15 | 30,10 | |||||
| 120,9 | 74,4 | 0,2 | 37,80 | |||||
| 145,4 | 89,4 | 0,24 | 46,10 | |||||
| 169,7 | 104,4 | 0,28 | 53,20 | |||||

| 00 | 00 | 00 | |||||
| 19,8 | 12,2 | 0,05 | 7,10 | 0,04 | 6,70 | 0,04 | 70 | |
| 45,4 | 28,0 | 0,1 | 16,70 | 0,1 | 15,70 | 0,1 | 160 | |
| 71,4 | 44,0 | 0,16 | 26,50 | 0,15 | 24,50 | 0,15 | 23,50 | |
| 96,4 | 59,3 | 0,19 | 36,20 | 0,2 | 33,10 | 0,2 | 31,20 | |
| 120,9 | 74,4 | 0,22 | 47,20 | 0,25 | 42,50 | 0,23 | 400 | |
| 145,4 | 89,4 | 0,24 | 62,20 | 0,28 | 520 | 0,27 | 480 | |
| 169,7 | 104,4 | Срыв | 0,32 | 62,50 | 0,32 | 56,50 | ||

| 00 | 00 | 00 | |||||
| 19,8 | 12,2 | 0,04 | 7,50 | 0,04 | 70 | 0,02 | 6,50 | |
| 45,4 | 28,0 | 0,07 | 170 | 0,08 | 160 | 0,06 | 150 | |
| 71,4 | 44,0 | 0,12 | 270 | 0,11 | 25,10 | 0,1 | 23,10 | |
| 96,4 | 59,3 | 0,17 | 36,90 | 0,15 | 33,20 | 0,13 | 31,50 | |
| 120,9 | 74,4 | 0,22 | 48,30 | 0,2 | 42,50 | 0,17 | 39,60 | |
| 145,4 | 89,4 | 0,26 | 630 | 0,27 | 520 | 0,21 | 47,60 | |
| 169,7 | 104,4 | Срыв | 0,32 | 620 | 0,26 | 560 | ||

| 00 | 00 | 00 | |||||
| 19,8 | 12,2 | 0,04 | 6,50 | 0,04 | 6,20 | 0,05 | 6,20 | |
| 45,4 | 28,0 | 0,09 | 15,10 | 0,1 | 14,70 | 0,1 | 14,40 | |
| 71,4 | 44,0 | 0,14 | 240 | 0,14 | 23,20 | 0,15 | 24,70 | |
| 96,4 | 59,3 | 0,18 | 32,50 | 0,19 | 32,30 | 0,21 | 30,30 | |
| 120,9 | 74,4 | 0,22 | 42,20 | 0,24 | 410 | 0,26 | 38,40 | |
| 145,4 | 89,4 | 0,26 | 53,30 | 0,28 | 500 | 0,3 | 46,20 | |
| 169,7 | 104,4 | 0,3 | 69,30 | 0,33 | 59,20 | 0,32 | 540 |
Примечание: Опыты проводились совместно с сотрудниками ВНИИЭ (г. Москва) с 16 апреля по 26 апреля 1988 г.
Таблица 2 Зависимость угла закручивания расщепленной фазы  от приложенного крутящего момента Мкр. Крутящий момент приложен в 1/4 пролета. Диаметр диска – 0,615 м. (провод АС-300/39, длина анкерного пролета
от приложенного крутящего момента Мкр. Крутящий момент приложен в 1/4 пролета. Диаметр диска – 0,615 м. (провод АС-300/39, длина анкерного пролета  м, число расщепления
м, число расщепления  шт.)
шт.)
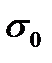 ,
даН /мм2 ,
даН /мм2
| Ргр, даН | Мкр,
даН  м м
| Число распорок
в пролете 
| Число распорок
в пролете 
| Число распорок
в пролете 
| |||
 , м , м
| 
|  , м , м
| 
|  , м , м
| 
| |||

| 00 | 00 | 00 | |||||
| 19,8 | 12,2 | 0,04 | 6,70 | 0,04 | 6,40 | 0,02 | 5,50 | |
| 45,4 | 28,0 | 0,01 | 15,70 | 0,1 | 13,40 | 0,06 | 130 | |
| 71,4 | 44,0 | 0,14 | 250 | 0,14 | 22,50 | 0,1 | 20,60 | |
| 96,4 | 59,3 | 0,2 | 340 | 0,18 | 30,10 | 0,14 | 280 | |
| 120,9 | 74,4 | 0,22 | 42,20 | 0,22 | 38,50 | 0,2 | 34,60 | |
| 145,4 | 89,4 | 0,25 | 520 | 0,26 | 47,40 | 0,24 | 41,70 | |
| 169,7 | 104,4 | 0,28 | 65,70 | 0,29 | 56,60 | 0,29 | 48,70 | |

| 00 | 00 | 00 | |||||
| 19,8 | 12,2 | 0,04 | 5,30 | 0,03 | 5,70 | 0,04 | 5,30 | |
| 45,4 | 28,0 | 0,08 | 13,20 | 0,08 | 13,20 | 0,08 | 100 | |
| 71,4 | 44,0 | 0,14 | 21,30 | 0,13 | 20,60 | 0,13 | 19,50 | |
| 96,4 | 59,3 | 0,18 | 29,20 | 0,18 | 27,70 | 0,18 | 260 | |
| 120,9 | 74,4 | 0,22 | 37,40 | 0,23 | 35,20 | 0,23 | 32,70 | |
| 145,4 | 89,4 | 0,27 | 46,30 | 0,26 | 42,70 | 0,28 | 39,40 | |
| 169,7 | 104,4 | 0,31 | 580 | 0,29 | 510 | 0,32 | 45,80 |
Примечание: Опыты проводились совместно с сотрудниками ВНИИЭ (г. Москва) с 1 по 10 июня 1988 г.
Таблица 3 Зависимость угла закручивания расщепленной фазы  от приложенного крутящего момента Мкр. Во всех опытах крутящий момент приложен в середине пролета. Диаметр диска – 0,433 м. (провод АС-300/39, длина анкерного пролета
от приложенного крутящего момента Мкр. Во всех опытах крутящий момент приложен в середине пролета. Диаметр диска – 0,433 м. (провод АС-300/39, длина анкерного пролета  м, число расщепления
м, число расщепления  шт, число распорок в пролете равна
шт, число распорок в пролете равна  шт.)
шт.)
| Ргр, даН | Мкр,
даН  м м
| 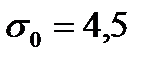
| 
| 
| 
| ||||
 , м , м
| 
|  , м , м
| 
|  , м , м
| 
|  , м , м
| 
| ||
| 00 | 00 | 00 | 00 | ||||||
| 10,4 | 4,5 | 0,04 | 6,50 | 0,04 | 80 | 0,04 | 7,70 | 0,03 | 5,80 |
| 8,7 | 0,07 | 13,50 | 0,06 | 14,80 | 0,07 | 14,40 | 0,06 | 11,30 | |
| 29,7 | 12,9 | 0,1 | 20,50 | 0,09 | 220 | 0,1 | 20,40 | 0,1 | 16,30 |
| 39,4 | 17,1 | 0,14 | 26,70 | 0,11 | 29,60 | 0,12 | 280 | 0,12 | 21,60 |
| 49,1 | 21,3 | 0,17 | 33,5 0 | 0,14 | 37,3 0 | 0,15 | 35 0 | 0,15 | 26,8 0 |
| 58,7 | 25,4 | 0,19 | 400 | 0,16 | 44,90 | 0,17 | 430 | 0,17 | 320 |
| 68,3 | 29,6 | 0,22 | 470 | 0,18 | 53,60 | 0,2 | 490 | 0,2 | 38,50 |
| 77,9 | 33,7 | 0,24 | 53,20 | 0,21 | 61,90 | 0,22 | 56,40 | 0,23 | 42,70 |
Примечание: Опыты проводились с 1 по 10 июня 1988 г.
Таблица 4 Зависимость угла закручивания расщепленной фазы  от приложенного крутящего момента Мкр. Во всех опытах крутящий момент приложен в середине пролета. (провод АС-240/32, длина анкерного пролета
от приложенного крутящего момента Мкр. Во всех опытах крутящий момент приложен в середине пролета. (провод АС-240/32, длина анкерного пролета  м, число расщепления
м, число расщепления  шт, число распорок в пролете
шт, число распорок в пролете  шт.)
шт.)
| Расстояние между проводами - 0,265 м. Диаметр диска – 0,3 м. | Расстояние между проводами - 0,65 м. Диаметр диска – 0,435 м. | |||||
| Ргр, даН | Мкр,
даН  м м
|  даН /мм2 даН /мм2
|  даН /мм2
даН /мм2
| Ргр, даН | Мкр,
даН  м м
|  даН /мм2
даН /мм2
|

| 
| 
| ||||
| 00 | 00 | 00 | ||||
| 0,3 | 80 | 60 | 0,87 | 20 | ||
| 0,6 | 150 | 140 | 1,74 | 50 | ||
| 0,9 | 210 | 210 | 2,61 | 80 | ||
| 1,2 | 290 | 260 | 3,48 | 110 | ||
| 1,5 | 36 0 | 32 0 | 4,35 | 150 | ||
| 1,8 | 430 | 400 | 5,22 | 19 0 | ||
| 2,1 | 530 | 480 | 6,09 | 220 | ||
| 2,4 | 630 | 590 | 6,96 | 260 | ||
| 2,7 | 83 0 | 670 | 7,83 | 300 | ||
| 9,2 | 2,76 | 970 | 8,7 | 340 | ||
| 9,3 | 2,79 | срыв | 9,57 | 370 | ||
| 9,6 | 2,88 | 870 | 10,44 | 420 | ||
| 11,31 | 460 | |||||
| 12,18 | 530 | |||||
| 13,05 | 580 | |||||
| 13,92 | 680 | |||||
| 14,36 | 850 |
Из вышеизложенного материала следует ряд важных выводов:
1) Экспериментальные и теоретические частоты поперечных колебаний провода в анкерном пролете оказываются достаточно близкими между собой при числе полуволн  . Такое заключение является достаточно общим, т.к. подтверждается для всех исследованных марок проводов и длин пролетов.
. Такое заключение является достаточно общим, т.к. подтверждается для всех исследованных марок проводов и длин пролетов.
2) При однополуволновых поперечных колебаниях проводов в анкерном пролете, в области малых напряжений эмпирические частоты оказываются более высокими, по сравнению с расчетными. По мере повышения напряжения в проводе расхождения между опытными и расчетными частотами уменьшается.
3) Экспериментальные и теоретические частоты поперечных однополуволновых колебаний проводов в 2-х пролетной системе практический совпадает. Близость опытных и расчетных частот обусловлены движением гирлянды изоляторов, следовательно, этот вывод также распространяется и для многопролетной системы.
4) На основе анализа частотных характеристик можно отметить, что уравнения колебания струны могут быть применены для анализа процесса пляски с числом полуволн  . Для однополуволновой пляски необходимо разработать более сложную модель, с учетом кривизны провисания проводов в пролете.
. Для однополуволновой пляски необходимо разработать более сложную модель, с учетом кривизны провисания проводов в пролете.
Дата добавления: 2015-08-20; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Шкала 13.Циклоид | | | Классификация видов опасных ситуаций социального характера |