Московский государственный университет приборостроения и информатики

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Реферат на тему: «Построение оптимизационных моделей»

Работу выполнил: студент 4-го

курса факультета УЭ-4

специальность 080100 «Коммерция»

Капитанчук А.П.

Работу проверил: Егоров Ю.Н.

Москва, 2015 г.

Введение

Успешность решения подавляющего большинства экономических задач зависит от наиболее эффективного способа использования ресурсов (денег, товаров, сырья, оборудования, рабочей силы и др.). Именно эффективностью использования, как правило, ограниченных, ресурсов определяется конечный результат деятельности любой экономической системы (фирмы, предприятия, отрасли).

Экономическая суть методов оптимизации заключается в том, что, исходя из наличия определенных ресурсов, выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя.

Актуальность темы обусловлена тем, что поиск оптимальных решений с помощью оптимизационных моделей необходим для коммерческой логистики. А коммерческая логистика есть организация управления экономическими системами в сфере товарного обращения. Следовательно, модели оптимизации отлично дополняют область логистики, и, по мнению автора, каждый, кто выбрал профессию логиста, обязан знать базовые оптимизационные модели.

1. Основная часть

1.1Понятие оптимизационных задач и оптимизационных моделей

Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.

Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.

Оптимальная или оптимизационная модель [optimization model] — экономико-математическая модель, которая охватывает некоторое число вариантов (технологических способов) производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти варианты, чтобы был найден лучший из них. [1]

Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов:

- управляемых переменных;

- неуправляемых переменных;

- формы функции (вида зависимости между ними).

Область допустимых решений это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Если система ограничений несовместима, то область допустимых решений является пустой. Ограничения подразделяются:

а) на линейные (^ I и II) и нелинейные (III и IV) (рис. 3.1);

б) детерминированные (А, В) и стохастические (группы кривых С _i ) (рис. 3.2).

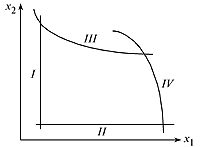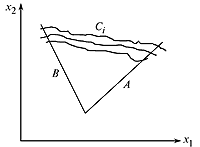Рисунок 3.1– Линейные и нелинейные ограничения

Рисунок 3.2– Детерминированные и стохастические ограничения

Стохастические ограничения являются возможными, вероятностными, случайными.

ОЗ решаются методами математического программирования, которые подразделяются на:

- линейное программирование;

- нелинейное программирование;

- динамическое программирование;

- целочисленное программирование;

- выпуклое программирование;

- исследование операций;

- геометрическое программирование и др.

Главная задача математического программирования это нахождение экстремума функций при ограничениях в форме уравнений и неравенств. [2]

1.2 Экономические основы оптимизации.

Оптимизационные (экстремальные) модели в экономике возникают при практической реализации принципа оптимальности в управлении.

Необходимым условием использования принципа оптимальности (оптимального подхода к планированию и управлению) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать те или иные управленческие решения. Именно такими, как правило, и являются ситуации, составляющие повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и загрузка контейнеров и т.д.).

Суть принципа оптимальности состоит в стремлении выбрать такое управленческое решение Х = (х ₁, х ₂, …, х_n), где х_j, j = 1,..., n, - его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.

«Наилучшим образом» здесь означает выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных управленческих решений. Традиционные критерии оптимальности в экстремальных моделях — «максимум прибыли», «минимум затрат», «максимум объема работ (услуг)» и др.

«Учитывало бы внутренние возможности и внешние условия производственной деятельности» означает, что на выбор управленческого решения (поведения) накладывается ряд условий, т.е. выбор X осуществляется из некоторой области возможных (допустимых) решений D.

Таким образом, реализовать на практике принцип оптимальности в планировании и управлении — это значит решить экстремальную задачу вида:

max (min) f (X) (1.1)

X ∈ D (1.2)

где f (X) - математическая запись критерия оптимальности - целевая функция.

1.3 Транспортная задача

Транспортная задача — задача о поиске оптимального распределения поставок однородного товара от поставщиков к потребителям при известных затратах на перевозку (тарифах) между пунктами отправления и назначения. Является задачей линейного программирования специального вида.

Значительная часть логистической операции на пути движения материального потока от первичного источника сырья до конечного потребителя осуществляется с помощью различных транспортных средств. Затраты на выполнение этих операций составляют до 50 процентов общих затрат на логистику.

Транспорт представляет собой систему, состоящую из двух под­систем: транспорт общего и не общего использования.

Транспорт общего использования обслуживает сферу обращения и населения. Его часто называют магистральным. Понятие транспор­та общего пользования охватывает: железнодорожный транспорт, водный (морской и речной), автомобильный, воздушный, трубопро­водный.

Транспорт не общего пользования включает внутрипроизводст­венный транспорт, а также транспортные средства всех видов, при­надлежащие не транспортным предприятиям.

Транспорт органично вписывается в производственные и торго­вые процессы. Поэтому транспортная составляющая участвует во многих задачах логистики. Вместе с тем существует достаточно са­мостоятельная транспортная область логистики.

К задачам транспортной логистики в первую очередь относят задачи, решение которых усиливает согласованность действий непо­средственных участников транспортного процесса. К таким задачам относятся:

- обеспечение технического соответствия участников транс­портного процесса (техническое соответствие означает согласован­ность как внутри отдельных видов, так и в межвидовом разрезе, ко­торая позволяет работать с контейнерами, пакетами);

- технологическая сопряженность - подразумевает применение единой технологии транспортировки, прямые перегрузки, беспере­грузочное сообщение:

- экономическая сопряженность - это общая методология ис­следования конъюнктуры рыка и построения тарифной системы, оз­начающие согласование экономических интересов участников транспортного процесса:

- использование единых систем планирования (разработка и применение различных планов графиков для различных видов транспорта);

К задачам транспортной логистики также относят:

- создание транспортных коридоров;

- выбор вида транспорта;

- выбор маршрута транспортировки грузов;

- составление расписаний. [4]

1.4 Общий вид транспортной задачи

На двух станциях отправления А₁ и А₂ сосредоточено соответственно а₁ и а₂ единиц некоторого однородного груза. Этот груз следует доставить в три пункта назначения B₁,B₂,B₃. Причем в каждый из них должно быть завезено соответственно b₁, b,₂ b₃ единиц этого груза. Стоимость перевозки единицы груза из пункта A_i в пункт B_j (обозначим C_ij) считаем заданной. Все данные полезно свести в табл. 1.

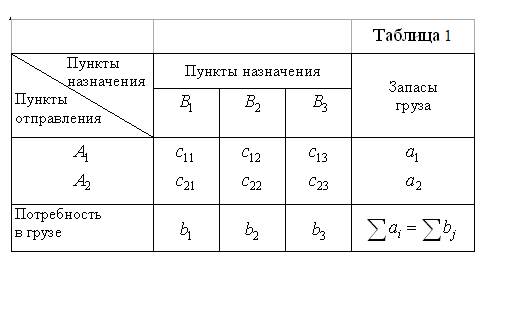
Будем считать, что общий запас грузов на станциях отправления равен суммарной потребности в этом грузе всех станций назначения. Следовательно,

a₁ +a₂ =b₁ +b₂ +b₃. (2.1)

Требуется составить такой план перевозок, при котором их общая стоимость была бы наименьшей.

Обозначим через x_ij количество единиц груза, предназначенного к отправке из пункта A_i в пункт B_j. Тогда количество груза, который планируется к доставке в пункт B₁ из пунктов A₁ и A₂, составит

x₁₁ + x₂₁.

Так как потребность в грузе B₁ равна b₁, то должно выполняться равенство:

x₁₁ + x₂₁ = b₁.

Аналогично получим равенства

x₁₂ + x₂₂ = b₂

x₁₃ +x₂₃ = b3

С другой стороны, общее количество груза, отправленного со станции A₁, выражается суммой

x₁₁ + x₁₂ + x₁₃ ,

которая, очевидно, обязана совпадать с запасом a₁ груза, сосредоточенным на этой станции, то есть

x₁₁ + x₁₂ + x₁₃ = a₁.

Подобно этому

x₂₁ + x₂₂ + x₂₃ = a₂

Полученные соотношения легче запомнить, если все величины свести в так называемую матрицу перевозок (см. табл. 2). Тогда легко проверить, что сумма всех x_ij, расположенных на i -ой строке, равна запасу a₁ в пункте назначения A₁. Сумма же всех x_ij из столбца j равна потребности b_j пункта назначения B_j.

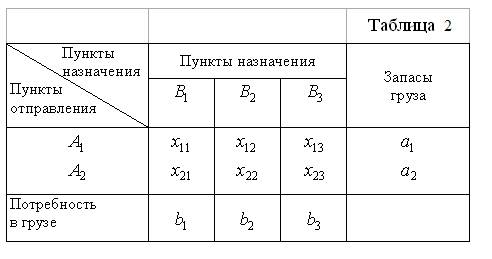
Из условий задачи с очевидностью вытекает, что общая стоимость F всех перевозок равна

.

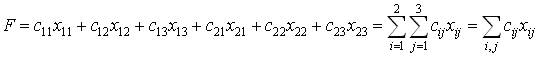Таким образом, математическая формулировка транспортной задачи (по критерию стоимости перевозок) такова. Задана система

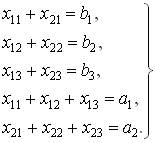(2.2)

пяти линейных алгебраических уравнений с шестью неизвестными и линейная форма

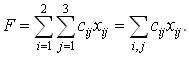(2.3)

Требуется среди всех неотрицательных решений x_ij системы (2.2) выбрать такое, при котором форма F минимизируется (достигает наименьшего значения). Отметим, что при решении транспортной задачи следует учитывать важное соотношение, вытекающее из самого условия задачи:

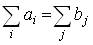. (2.1') [3]

Заключение

В заключение к реферату автор отмечает важность оптимизационных моделей. Они могут применяться в различных областях экономики, в том числе и в логистике. Умение пользоваться ими позволяет логисту создать варианты оптимального использования ресурсов, имеющихся у организации. Отдельно автор подчеркивает транспортную задачу. Хотя эта модель не дает логисту точных данных о том, как можно снизить издержки организации, она может дать ему варианты для использования ресурсов организации с минимальными потерями для нее. Транспортная задача рассчитывает ту сумму, которую организация затратит в случае выбора того или иного пути поставки товара.

Список источников

1. Лопатников Л. И., Экономико-математический словарь: Словарь современной экономической науки. — 5-е изд., перераб. и доп. — М.: Дело, 2003. — 520 с.;

2. Мурлин А.Г. «Компьютерное моделирование. Конспект лекций», М.: Кафедра вычислительной техники и АСУ, Краснодар, 2007

3. Рейзлин В.И., «Численные методы оптимизации», - Изд. ТПУ, 2013;

4. Д. Шрайбфедер, «Эффективное управление запасами», - Изд. Альпина Бизнес Букс, - М., 2006, 306 стр.

Дата добавления: 2015-08-20