Eigenvalues and diagonalization

A task related to eigenvalues, eigenvectors, general or orthogonal diagonalization:

a) For the given matrix, find eigenvalues and bases for the eigenspaces.

b) Determine, whether the given non-symmetric matrix is diagonalizable. If so, find a matrix that diagonalizes and determine .

c) Find a matrix that orthogonally diagonalizes the given symmetric matrix and determine .

Each variant will include exactly one type of tasks from a)-c)

Example.

For the given matrix, find eigenvalues and bases for the eigenspaces

Solution (in Russian).

Чтобы найти собственные значения матрицы , решаем характеристическое уравнение , т.е. . Последовательно получаем, что 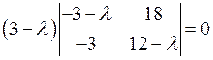, , 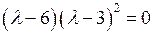. Поэтому собственными значениями матрицы являются и .

Найдем соответствующие собственные векторы. При характеристическая матрица принимает вид . Решая соответствующую систему однородных уравнений, получим 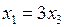. Общее решение системы . Если то 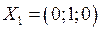, а если то , и множество собственных векторов, соответствующих собственному значению , может быть записано в виде .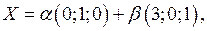

При получим систему ~ ~ , т.е. и , . Общее решение системы . Таким образом, множество собственных векторов, соответствующих собственному значению , записывается в виде .

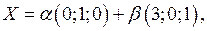
Ответ: Собственные значения и . При , при . Векторы (0;1;0), (3;0;1) образуют базис (двумерного) собственного подпространства, соответствующего собственному значению . Вектор (2;-1;1) образует базис (одномерного) собственного подпространства, соответствующего собственному значению .

Example. Determine, whether the matrix is diagonalizable. If so, find a matrix that diagonalizes and determine .

Example. Find a matrix that orthogonally diagonalizes the given symmetric matrix and determine .

7. One theoretical question from the “Full list of theoretical questions for the exam”.

Дата добавления: 2015-08-03