Black Holes

Black holes are one of the most fascinating objects predicted by Einstein's theory of general relativity. Black holes have an interesting history and they have been a source of many theoretical surprises which have led to a better understanding of the nature of space-time.

Let us begin by considering Newton's theory of gravity. Here on the surface of the earth we can feel the pull of gravity. If we throw a stone up, it comes back down due to the force of gravity. Could we throw an object up so that it would not come back down? Yes. If we throw it with a velocity higher than 11 km/s, then it will leave the gravitational field of the earth. This "escape velocity" depends on the mass and the radius of the Earth. If the Earth were more massive and with the same radius, then the escape velocity would be higher. One can then ask: What would happen if we had an object that is so dense and so massive that the escape velocity were faster than the speed of light? Then it would look black, no light could escape from it. For example, a star with a size smaller than

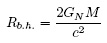
would look black. Here G_N is Newton's constant and c is the speed of light.

If you are not familiar with formulas, let me give you a few examples. In order for an object of the mass of the Earth to become a black hole, it would have to be smaller than one centimeter. An object with the mass of the sun would have to be concentrated in a region smaller than one kilometer. This was pointed out in the 1800's by P. Laplace, but no one paid much attention to it.

With the advent of Special Relativity in 1905, we learned that the speed of light is not like any other ordinary speed. It is the cosmic speed limit: nothing can travel faster than light. Einstein's theory of relativity also tells us that space and time are intimately connected. Time flows differently for observers who are moving relative to each other. Suppose you are standing by a street watching the cars go by. Time flows differently for people in the car than it does for you. Suppose that you see two separate street lights turning red at the same time. For the drivers they would not turn red at the same time. This is, of course, after taking into account the time it takes for light to reach the eyes of both observers. Both see light travelling at the speed of light, but they see time flowing different. Time is relative, the speed of light is absolute. This is counter intuitive because it is a very small effect for us, since we usually travel at speeds much smaller than the speed of light and we do not keep track of time very precisely. This is an effect which is seen all the time in particle accelerators. Particles live much longer when they are moving at speeds close to the speed of light.

Space and time are put together into a single concept space-time. Time is perceived differently by two observers that are moving relative to each other. Both observers see the same space-time. There are precise formulas that enable us to relate the observations of these two observers.

Let us now go back to gravity. Gravity has one very special feature that was discovered by Galileo: all objects fall in the same way after we remove the effects of air resistance. In the vacuum a feather and a stone fall together. This does not happen for other forces. A particle in an electric field will move differently if its mass or its charge is changed. In Newton's theory of gravity, the reason that all particles fall in the same way is due to the fact that the gravitational force is proportional to the mass. This is sometimes called the "equivalence principle."

Einstein realized that Newton's theory was not compatible with special relativity, since in Newton's theory, the gravitational force propagates instantaneously. In 1915 Einstein solved this problem in a way that also naturally incorporates the equivalence principle. He named this theory General Relativity. He proposed that gravity is due to the curvature of space-time. Particles in a curved space-time follow the shortest lines. Lines that are initially parallel on a curved space might later move toward each other. For example, two meridian lines at the Earth's equator start out parallel at the equator, but they intersect at the North Pole. The shape of space-time depends on the matter that moves on it. General relativity implies that the flow of time depends on the gravitational field. Therefore, two people living in the same building, one on the top floor and one on the bottom floor, would see time flowing differently. Time would flow more slowly for the person on the bottom floor. This is a very tiny effect for a building here on Earth — it is an effect of one part in 10¹⁵. What we learn is that a massive object warps space and time. In particular, this means that time close to a massive object flows more slowly than time far away.

Physicists always try to study the simplest situations first. So in 1916, shortly after general relativity was invented, a young German, named Karl Schwarzschild, found the simplest spherically symmetric solution of Einstein's equations. These equations describe a particular geometry which was thought to be the geometry generated by a point-like mass. Instead of saying what the geometry is, let us concentrate on one of its features: the rate at which stationary clocks tic. A clock at the surface of the sun runs slower by one part in a million than a clock far away. A clock on the surface of a neutron star runs at 70% of the speed of a clock far away from the star. In this case we see that it is a large effect. The solution that Schwarzschild found indicated that a clock at the "center" would completely stop. At first most physicists thought that this was an unphysical result, a product of an overly simplified analysis.

Further studies showed that the "center" of Schwarzschild's solution is, in fact, a completely smooth surface. An observer that is travelling through space-time could go through this region without feeling anything strange or peculiar. The people who stay outside the black hole see that all signals coming from the falling observer slow down until they eventually die out for all practical purposes. The surface where stationary clocks slow down to zero is called a "horizon." This surface marks a point of no return. An observer who crosses this surface will not be able to come back out again and will crush into a "singularity" in the interior. The singularity is a region of very high space-time curvature that will rip him apart. It turns out that the size of a black hole in Einstein's theory is still given by the formula that Laplace computed in Newton's theory, but the physical interpretation is very different.

Black holes can form in astrophysical processes when stars that are a few times more massive than the sun run out of their nuclear fuel and implode under their gravitational force. There is a great deal of observational evidence that there are some black holes out there in the universe. These astrophysical black holes come in two main types. Some have a mass a few times higher than the mass of the sun and are produced by stellar collapse. Since black holes are black, it is very hard to see them. Sometimes we are fortunate to have some gas fall into the black hole. As it falls, this gas heats up and emits a characteristic radiation that is then detected. This gas can come from another star that is orbiting the black hole. In other words, we can start with two stars that are orbiting each other and one collapses and turns into a black hole. Then the gas from the other can start falling into the black hole. There are also much more massive black holes at the center of galaxies. These have the mass of a billion suns. Again when matter falls into these black holes it can heat up and emit radiation that is eventually detected by us here on Earth. All big galaxies, like ours, are believed to have a black hole in the center.

The focus of this talk is not to describe astrophysical black holes, but to explore the implications of black holes for the structure of space-time.

According to Einstein's theory a black hole is a hole in space-time, once you fall in you cannot come back again. Whatever is thrown into a black hole is forever lost.

Black holes have very interesting universal properties. When a star collapses into a black hole its final form depends only on two parameters: the mass and the angular momentum. So black holes are universal, namely they are independent of the peculiar detailed properties of the matter that formed them. Regardless of the chemical composition of the initial star, we always get the same black hole. So black holes depend only on the theory of gravity and do not depend on the details of the other forces.

Another peculiar feature of black holes is the following: suppose you have some process where black holes are involved. For example, we can consider the collision of two black holes. The black holes collide and form a larger black hole. Incidentally, this process can emit gravitational waves and there are some detectors trying to measure them. This process is quite hard to compute, one has to solve rather complicated equations. Nevertheless, there is some simple result. The area of the final black hole is always bigger than the sum of the areas of the initial black hole. The area always increases. This is called the "area theorem" and it was proven by Hawking in 1970.

Дата добавления: 2015-08-03