Уравнение силы и моментов, действующих на ракету.

Дифференциальное уравнение движения для крылатой ракеты.

Управляемая ракета при движении по траектории к цели, подчинены следующим факторам:

1) начальные условия запуска;

2) траектория движения цели в момент прицеливания;

3) методы наведения ракеты;

4) конструктивные параметры ракеты;

5) свойства воздушной среды.

В теории динамики ракеты выделяется такая группа:

· кинематическое исследование движения ракеты (вектор тяги);

· динамическое исследование движения ракеты (с учетом всей силы).

Уравнение силы и моментов, действующих на ракету.

1. Уравнение силы на ось X скоростной СК.

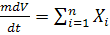(9.4.1)

2. Уравнение сил на ось 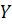скоростной СК.

(9.4.2)

3. Уравнение сил на ось скоростной СК.

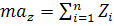(9.4.3)

4. Уравнение моментов относительно оси связанной СК.

(9.4.4)

5. Уравнение моментов относительно оси 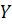связанной СК.

(9.4.5)

6. Уравнение моментов относительно оси связанной СК.

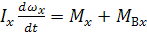(9.4.6)

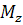, , - проекция аэродинамического момента;

, , – проекция возмущающих моментов.

Кинематические уравнения отображают в математической форме движение центра масс ракеты и цели.

рис. 9.2

Р – центр масс ракеты;

Ц – центр масс цели;

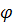- угол линии визирования;

- расстояние между центрами масс ракеты и цели;

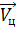- вектор скорости цели;

- вектор скорости ракеты;

- угол наклона траектории ракеты;

- угол наклона траектории цели.

Запишем первое кинематическое уравнение. Для этого спроектируем скорость ракеты и цели на линию, которая соединяет центры масс ракеты и цели.

(9.5)

При неравенстве нормальной составной скорости и цели, будут возникать поворот линии визирования с некоторой угловой скоростью.

Запишем второе уравнение, которое характеризует поворот:

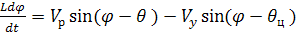(9.6)

Уравнение (9.5) и (9.6) называются кинематическими уравнениями движения центра масс.

Эти соотношения дальше применяются для описания динамики управляемой ракеты.

Дата добавления: 2015-08-02