Соответствия и их свойства

СООТВЕТСТВИЯ

1. Соответствия и их свойства.

Соответствия и их свойства

Соответствие - способ задания взаимосвязей, взаимодействий между элементами множества (наряду с отношениями). Частными случаями соответствий являются функции, отображения, преобразования, операция и др.

Соответствием между множествами А и В называется подмножество G прямого произведения этих множеств: G Í A ´ B. Если (a, b)Î G, то говорят, что " b соответствует а при соответствии G ".

Область определения соответствия G - множество пр₁ G = { а:(a, b)Î G}. Область значений соответствия G -множество пр₂ G = { b:(a, b)Î G} (рис.1).

Свойства соответствий G Í A ´ B:

• Всюду (полностью) определенное соответствие - если пр₁ G = А. Частично определенное соответствие - в противном случае.

• Сюръективное соответствие - если пр₂ G = В.

Образом элементаа в множество В при соответствии G называется множество всех b Î В, соответствующих элементу а Î А. Прообразом элемента b в множество А при соответствии G называется множество всех а Î А, которым соответствует b Î В.

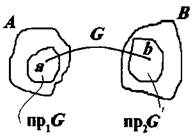
Рис.1

Образом множества С Î пр₁ G называется объединение образов всех элементов а Î С. Прообразом множества D Î пр₂ G называется объединение прообразов всех элементов b Î D.

• Функциональное (однозначное) соответствие - если образом любого элемента а из области определения np₁ G является единственный элемент b из области значений пр₂ G.

• Взаимно однозначное соответствие - если оно:

а) всюду определено;

б) сюръективно;

в) функционально;

г) прообразом любого элемента b из области значений пр₂ G является единственный элемент а из области определения пр₁ G.

Если между множествами А и В существует взаимно однозначное соответствие, то мощности этих множеств равны, т.е. | А | = | В |. В таком случае говорят, что множества А и В равномощны. Этот факт позволяет:

• установить равенство мощностей двух множеств, не вычисляя этих множеств;

• вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется.

Множества, равномощные множеству натуральных чисел N, называются счетными. Множества, равномощные множеству вещественных чисел R, называются континуальными.

Пример 1

Пусть G - множество всех пар действительных чисел (х, у), удовлетворяющих соотношению

(х -3)² + (у - 2)² £ 1. Графически такое соответствие G представляет собой круг радиуса 1 с центром в точке (3, 2). Таким образом, круг G задает соответствие между R и R (осью абсцисс и осью ординат, рис.2).

Определите, чему равны:

а) образы и прообразы чисел 2, 3, 4;

б) образы и прообразы отрезков [2,3], [2,4].

Каковы свойства соответствия G?

а) Образом числа 2 Î пр₁ G (на оси абсцисс) при соответствии G (см. рис.2) является единственное число 2 Î пр₂ G (на оси ординат).

Образ числа 3 при соответствии G есть множество всех действительных чисел отрезка [1, 3], а образ числа 4-число 3.

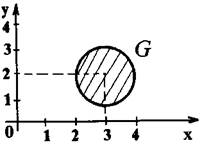
Рис.2

Прообразом числа 2 Î пр₂ G (на оси ординат) при соответствии G будет множество всех действительных чисел отрезка [2, 4] Î пр₁ G (на оси абсцисс), прообразом числа 3 при соответствии G — число 3, а прообраза числа 4 при соответствии G не существует.

б) Образом множества чисел отрезка [2,3] Î пр₁ G является объединение образов всех чисел отрезка, т.е. отрезок [1, 3] Í пр₂ G. Аналогично образом отрезка [2,4] будет отрезок [1,3] при соответствии G.

Прообраз отрезка [2,3] при соответствии G-это отрезок [2,4], а прообраз отрезка [2,4] - также [2,4].

Если допустить, что соответствие G установлено на множестве действительных чисел, т.е. G Í R ´ R, то оно является:

• частично определенным, так как пр₁ G ¹ R (пр₁ G Ì R);

• не сюръективным, поскольку пр₁ G ¹ R (пр₂ G Ì R);

• не функциональным, ибо для любого числа отрезка [2,4] = пр₁ G (кроме чисел 2, 4) отсутствует единственность образа;

• не взаимно однозначным, так как отсутствуют необходимые условия: G не является всюду определенным на R, не сюръективно, не функционально, а также для любого числа отрезка [1,3] = пр₂ G (кроме чисел 1, 3) отсутствует единственность прообраза.

Если определить соответствие G Í [2, 4] ´ [1, 3], то, очевидно, оно будет всюду определенным и сюръективным, однако останется не функциональным и не взаимно однозначным.

Пример 2

Пусть G - множество точек прямой линии, удовлетворяющей соотношению х - 2 = у при х, у ³0 (рис.3). Каковы свойства соответствия G?

1. Если соответствие G задано на множестве действительных чисел, т.е. G Í R ´ R, то G:

• частично определено, так как пр₁ G = [2, ¥) Ì R;

• не сюръективно, поскольку пр₂ G = R₊ Ì R, где R₊ = [0, ¥] - множество всех положительных действительных чисел с нулем;

Рис.3

• функционально, ибо любому х из области определения соответствует единственный у из области значений, т.е. для соответствия G имеет место единственность образа для любого х Î пр₁ G;

• не взаимно однозначно, так как не выполняются условия - всюду определенности и сюръективности.

2. В случае, если соответствие G задано на множестве R₊ с нулем, т.е. G Í R₊ ´ R₊, тогда соответствие G:

• частично определено, так как пр₁ G = [2, ¥) и пр₁ G Í R₊;

• сюръективно, поскольку пр₂ G = R₊;

• функционально;

• не взаимно однозначно, так как не выполняется условие - всюду определенности.

3. При G Í [2, ¥) ´ R₊ соответствие G:

• всюду определено;

• сюръективно;

• функционально;

• взаимно однозначно, так как наряду с выполнением перечисленных выше условий имеет место также единственность прообраза для любого у Î пр₂ G.

Пример 3

Англо-русский словарь устанавливает соответствие между множествами английских и русских слов. Каковы свойства этого соответствия?

Данное соответствие не является:

• всюду определенным (всегда можно найти английское слово, не содержащееся в словаре);

• сюръективным (по отношению русских слов, имеющихся в словаре);

• функциональным (одному английскому слову ставится в соответствие, как правило, несколько русских);

• взаимно однозначным (в силу предыдущего).

Пример 4

Пусть множества b(U), где U= {а, b, с}, и B ₃ определены следующим образом:

b(U) - множество всех подмножеств (булеан) множества U= {а, b, с};

В ₃ - множество всех двоичных векторов длины 3, т.е. В ₃ =А ´ А ´ А, где A = {0, 1}.

Показать, что между множествами b(U) и В ₃где U= {a, b, с}, имеет место взаимно однозначное соответствие.

b(U) = {Æ, {а}, {b}, {с}, {а, b}, {а, с}, {b, с}, {а, b, с}};

| b(U) | = 8.

В ₃= {(000), (001), (010), (011), (100), (101), (110), (111)};

| В ₃ | = 8

(для упрощения обозначений запятые между компонентами векторов опущены).

Установим следующее соответствие G между множествами из b(U)и векторами из B ₃:

• если в множестве из b(U) присутствует элемент а, то в соответствующем ему векторе из B ₃ первая компонента равна 1, а если отсутствует - то 0;

• если в множестве из b(U) присутствует элемент b, то в соответствующем ему векторе из B ₃ вторая компонента равна 1, а если отсутствует - то 0;

• аналогичное соответствие установим между элементом с в множестве из b(U) и значением третьей компоненты вектора из В ₃.

Например, множеству {b} из b(U) соответствует вектор (010) из В ₃множеству {а, с} - вектор (101) и т.д.:

G:Æ ® (000), {а} ® (100), {b} ® (010), {с} ® (001), {а, b} ®(110), {а,с} ®(101), {a, с} ® (011), {а, b, с} ®(111).

Установленное, таким образом соответствие G является взаимно однозначным, так как выполняются все условия для взаимно однозначного соответствия.

Пример 5

Используя определение равномощности множеств, покажите, что множество М ₂ n натуральных чисел, являющихся степенями двойки, счётно.

Для доказательства следует установить взаимно однозначное соответствие между множествами М ₂ n и N. Если каждому натуральному п Î N поставить в соответствие число 2 ^{n -1} Î М ₂ n, то установленное таким образом соответствие G Î N ´ M ₂ n, очевидно, является взаимно однозначным (удовлетворяет всем требованиям для взаимно однозначного соответствия) и представляет множество всех векторов G = {(п, 2 ^{n -1}): п Î N }. А так как мощность множества N cчетна, то из установленной взаимной однозначности между множествами N и М ₂ n согласно определению равномощности бесконечных множеств, следует, что множество М ₂ n также счетно.

---

Дата добавления: 2015-08-03