Решение. Задача 5. Для поставленной задачи выполнить следующие задания:

Вариант 12

Задача 5. Для поставленной задачи выполнить следующие задания:

max( -4 +3 +2)

1) Решить задачу методом сопряженных направлений взяв в качестве начальной точку х⁰= ;

2) Проиллюстрировать графически результаты выполнения (1).

Решение.

1) В качестве начальной берем точку 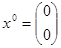. Выбираем

произвольный вектор 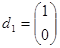. Далее строим линейное многообразие , натянутое на по правилу , где :

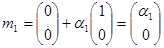
2) Найдем точку максимума исходной функции в линейном

многообразии : . Для этого необходимо найти .

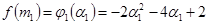
Для нахождения максимума функции , найдем её производную и приравняем ее к нулю:

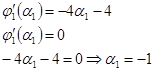
Проверим точку :

Следовательно, - точка максимума функции в линейном многообразии .

3) Далее делаем расширяющий шаг градиентным методом и

находим точку , где :

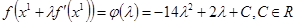
Для нахождения максимума функции , найдем её производную и приравняем ее к нулю:

Проверим точку :

Следовательно, - точка максимума функции .

Результат расширяющего шага:

.

4) Строим линейное многообразие , натянутое на вектор , по

правилу , где :

.

Найдем точку максимума исходной функции в линейном

многообразии : . Для этого необходимо найти .

.

Для нахождения максимума функции , найдем её производную и приравняем ее к нулю:

Проверим точку :

Следовательно, - точка максимума функции , а - точка максимума функции в линейном многообразии .

Получим новый вектор: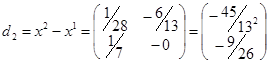

Проверка:

а)

Следовательно, условие выполнено.

б)

Условие выполнено.

5) Строим линейное многообразие , натянутое на вектор ,по

правилу , где :

.

Найдем точку максимума исходной функции в линейном

многообразии : 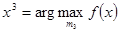. Для этого необходимо найти .

.

Для нахождения максимума функции 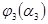, найдем её производную и приравняем ее к нулю:

Проверим точку :

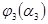Следовательно, - точка максимума функции , а .

6) Проверяем: . Следовательно

точка - точка экстремума в функции в линейном многообразии, натянутым на Q-сопряженные вектора и .

7)

Дата добавления: 2015-08-02