
Читайте также:
|
Молекулы являются микроскопическими объектами и их свойства описываются в терминах квантовой механики, а именно - уравнением Шрёдингера
ĤΨ = ΕΨ, (1.1)
где Ĥ – гамильтониан системы; Е и Ψ – собственные значения энергии и собственные волновые функции соответственно.
Точное решение уравнения Шрёдингера для многочастичной системы невозможно, поэтому используют ряд приближений. Прежде всего учитывают иерархию движений, характерных для молекул:
1. Кинетическая энергия поступательного движения молекулы (предполагается, что вещество находится в газообразном состоянии) описывается выражением
Τ = 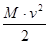 , (1.2)
, (1.2)
где v – скорость центра инерции (масс) молекулы; М – суммарная масса молекулы. Координаты центра инерции определяются уравнением
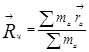 , (1.3)
, (1.3)
где  - соответственно массы и координаты всех частиц, входящих в молекулу. Эта форма движения хорошо описывается классической механикой во всём диапазоне температур – на одну поступательную степень свободы молекулы в среднем приходится энергия, равная
- соответственно массы и координаты всех частиц, входящих в молекулу. Эта форма движения хорошо описывается классической механикой во всём диапазоне температур – на одну поступательную степень свободы молекулы в среднем приходится энергия, равная  .
.
2. Кинетическая энергия вращательного движения – характеризует вращение молекулы как целого относительно центра инерции
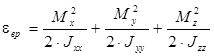 , (1.4)
, (1.4)
где Jii и Mi – моменты инерции и моменты импульса относительно главных осей. При температурах выше ~ 10 К квантовыми эффектами вращательного движения с достаточно высокой степенью точности также можно пренебречь и считать, что на каждую вращательную степень свободы в среднем приходится энергия, равная  .
.
3. Внутримолекулярное движение – включает в себя кинетическую энергию ядер и электронов относительно центра инерции плюс потенциальную энергию межчастичного взаимодействия. Потенциальная энергия взаимодействия частиц с внешними полями может быть учтена (в зависимости от рассматриваемой системы частиц) либо как воздействие внешних полей на молекулу в целом, либо включена во внутримолекулярное взаимодействие. Для описания внутримолекулярного движения нужно решить уравнение Шрёдингера
Ĥ( )Ψ(
)Ψ( ) = ΕΨ(
) = ΕΨ( ), (1.5)
), (1.5)
где Ĥ( ) и Ψ(
) и Ψ( ) – электронно-ядерный гамильтониан и электронно-ядерная волновая функция; {
) – электронно-ядерный гамильтониан и электронно-ядерная волновая функция; {  } и {
} и { 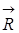 } – совокупность координат электронов и ядер соответственно (начало координат находится в центре инерции).
} – совокупность координат электронов и ядер соответственно (начало координат находится в центре инерции).
Решение уравнения (1) представляет огромные трудности. Поэтому при его решении используется ряд приближений.
Адиабатическое приближение. Его суть заключается в том, что, благодаря большой разнице в скоростях электронной и ядерной подсистем (как следствие огромного различия в массах электронов и ядер), можно разделить переменные в уравнении (1.5). Сначала нужно решить уравнение Шредингера для электронной подсистемы при фиксированных координатах ядер
Ĥ эл (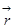 │
│  )Ψ(
)Ψ(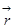 │
│  ) = ε эл (
) = ε эл ( )Ψ(
)Ψ(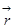 │
│  ), (1.6)
), (1.6)
а затем решать уравнение Шрёдингера для ядерной подсистемы, используя зависимость ε эл ( ) в качестве составляющей потенциальной энергии ядер
) в качестве составляющей потенциальной энергии ядер
[Ĥ яд ( ) + ε эл (
) + ε эл ( )]Φ(
)]Φ( ) = ε яд Φ(
) = ε яд Φ( ). (1.7)
). (1.7)
Решение уравнения (1.7) даёт информацию о колебательных спектрах и колебательных волновых функциях системы, но так как в данных методических указаниях речь идёт об электронной структуре молекул, то основное внимание нужно уделить решению уравнения (1.6). Обычно его решают при равновесных значениях ядерных координат, поэтому индекс {  } можно опустить
} можно опустить
Ĥ эл Ψ( ) = ε эл Ψ(
) = ε эл Ψ( ). (1.8)
). (1.8)
Одноэлектронное приближение. Решение уравнения Шрёдингера (1.8) для электронной подсистемы всё ещё представляет огромные трудности, поэтому для его упрощения полагают, что каждый электрон в молекуле движется независимо от других электронов, а межэлектронное взаимодействие моделируется некоторым самосогласованным эффективным полем. Это предположение позволяет перейти от решения сложной многоэлектронной задачи к решению одноэлектронного уравнения Шрёдингера
ĥψ(r) = εψ(r), (1.9)
где ĥ и ψ(r) – одноэлектронный гамильтониан и одноэлектронная волновая функция (молекулярная орбиталь).
Существует много методов нахождения молекулярных орбиталей (МО), использующих дальнейшие упрощения выражения (1.9). Одним из самых первых (и до сих пор востребованным) является метод молекулярных орбиталей как линейной комбинации атомных орбиталей (МО ЛКАО). В рамках этого метода решение уравнения (1.9) ищут в виде линейной комбинации атомных орбиталей {χμ}, которые считаются известными (их либо берут в справочной литературе, либо предварительно рассчитывают для каждого атома, входящего в молекулу). Таким образом, можно записать
ψi =  c iμχμ, (1.10)
c iμχμ, (1.10)
где N – размерность базиса (количество) исходных атомных орбиталей (АО). В этом случае задача нахождения молекулярной орбитали ψi сводится к задаче нахождения коэффициентов разложения c iμ. Уравнение (1.10) описывает линейное преобразование исходного базиса атомных орбиталей {χμ} в искомый базис молекулярных орбиталей {ψi} (его размерность также равна N). Решение уравнения Шрёдингера (1.9) в этом случае сводится к решению системы N линейных уравнений с N неизвестными (уравнения Рутаана)
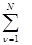 с iν(Н μν – εi S μν) = 0 (μ = 1,…N) (1.11)
с iν(Н μν – εi S μν) = 0 (μ = 1,…N) (1.11)
где Н μν и S μν – соответствующие матричные элементы гамильтониана и интегралы перекрывания.
Существует множество расчётных схем решения системы уравнений (1.11), отличающихся друг от друга ограничениями, накладываемыми на оценку величин F μν и S μν. Некоторые из них будут рассмотрены ниже.
Интерпретация решения уравнения Шрёдингера для электронной подсистемы молекулы. В качестве решения вышеприведенного уравнения получают совокупность собственных значений энергии {εi} и матрицу коэффициентов { с iν}, каждый из которых численно равен вкладу ν-АО в i-МО. Среди всех МО особую роль играют верхняя заполненная молекулярная орбиталь (ВЗМО) и нижняя свободная молекулярная орбиталь (НСМО). Первая из них характеризует донорные свойства молекулы, вторая – акцепторные.
Для каждой из указанной МО полезно знать распределение электронной плотности по атомам и характер химического связывания. Эта информация необходима для определения наиболее реакционноспособного атома при донорном или акцепторном взаимодействии. Кроме того, она позволяет установить, является ли данная МО связывающей или разрыхляющей (несвязывающей).
Итак, рассмотрим i-ю молекулярную орбиталь ψi =  c iμχμ, для которой должно соблюдаться условие нормировки
c iμχμ, для которой должно соблюдаться условие нормировки 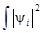 dV = 1. Заселённость ν-АО в данной МО оценивается величиной ρiν (при условии, что на данной МО находятся 2 электрона)
dV = 1. Заселённость ν-АО в данной МО оценивается величиной ρiν (при условии, что на данной МО находятся 2 электрона)
ρiν = 2·(c iν2 + 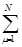 c iν c iμ S μν). (1.12)
c iν c iμ S μν). (1.12)
Заселённость атома А в данной МО ρiА находится путём суммирования ρiν по всем v-АО, центрированным на атоме А.
ρiА = 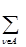 ρiν . (1.13)
ρiν . (1.13)
Для оценки связывающего или разрыхляющего характера взаимодействия ν-АО и μ-АО в рассматриваемой i-МО вычисляют заселённость перекрывания:
ημν(i) = 2 c iν c iμ S μν. (1.14)
Если ημν(i) < 0, то говорят о разрыхляющем характере взаимодействия. Если ημν(i) > 0, то говорят о связывающем характере взаимодействия. Естественно, что в данном случае ν-АО и μ-АО должны быть центрированы на разных атомах, так как в противном случае S μν = δμν.
Если соотношения (1.12)-(1.14) просуммировать по всем занятым молекулярным орбиталям, то можно получить соответствующие характеристики для всей молекулы в целом, а не для отдельной МО:
заселённость ν-АО: ρ ν =  (1.15)
(1.15)
количество электронов на атоме А: ρА =  (1.16)
(1.16)
заряд атома А: qА = ZA ‑ ρА (ZA – число протонов в атоме) (1.17)
заселённость перекрывания (ЗП) ν-АО и μ-АО: ημν = 2 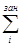 ημν(i) (1.18)
ημν(i) (1.18)
суммарная ЗП атомов А и В: η АВ =  ημν (1.19)
ημν (1.19)
(суммирование проводят по всем μ-АО, центрированным на атоме А, и по всем ν-АО, центрированным на атоме В).
Для характеристики свойств молекулы также часто используют следующие величины:
матрица электронной плотности P μν =  n i c iν c iμ (1.20)
n i c iν c iμ (1.20)
(ni – заселённость i-МО)
валентность связи А‑В VAB = 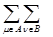 P μν2 (1.21)
P μν2 (1.21)
валентность атома А в молекуле VA = 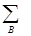 VAB (1.22)
VAB (1.22)
Дата добавления: 2015-08-02; просмотров: 48 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Язык, речь | | | СЕКРЕТЫ НАНЕСЕНИЯ ЖИДКОЙ ПОДВОДКИ-КАРАНДАША |