тов в классе полиномиальных функций.

Пусть известны значения yi в узлах xi, i = 0; 1; 2; …; n, y(a0; a1;…; am; x)

- функция, зависящая от параметров a0; a1; …; am. Рассмотрим функцию S:

Выберем параметры a0; a1;…; am так, чтобы минимизировать S, т.е. сумму квадратов невязок.

Отсюда получаем систему уравнений:

Эту систему уравнений (часто нелинейную) можно решить методом Ньютона.

Рассмотрим подробнее случай, когда функция y(x) является многочленом степени m:

Мы получаем СЛАУ:

Приводим её к виду:

Введём коэффициенты:

Получим систему линейных алгебраических уравнений:

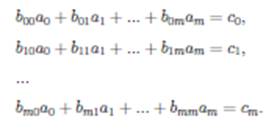
Эта система решается методом Гаусса.

Пример. Пусть даны точки:

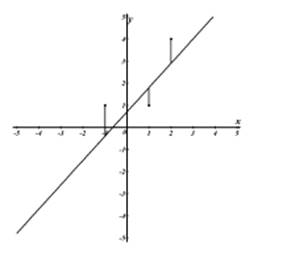
1. Найдем методом наименьших квадратов прямую y(x) = a0 + a1x, на

которой минимизируется сумма квадратов невязок. Получаем систе-му уравнений:

Отсюда y(x) = 0, 7 + 1, 1x

2. Найдем методом наименьших квадратов параболу

p(x) = a0+a1x+a2x2, на которой минимизируется сумма квадратов не- вязок. П0лучаем систему уравнений:

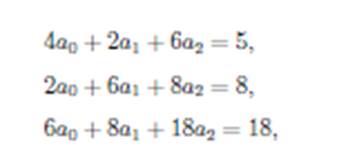
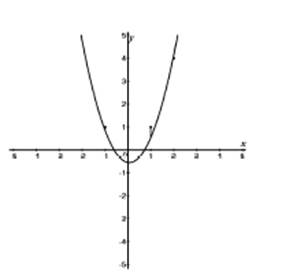
Решив ее, найдем, что p(x) = 1, 25x*x-0,15x +0, 55.

Дата добавления: 2015-08-02