Читайте также:
|
Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.
Исследование вариации в статистике имеет важное значение, т.к. дает возможность оценить степень воздействия на данный признак других варьирующих признаков. Определение вариации необходимо при организации выборочного наблюдения, построения статистических моделей, разработке материалов экспертных опросов и т.д.
Средняя величина — это обобщающая характеристика признака изучаемой совокупности. Она не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней. Поэтому для характеристики колеблемости признака используют показатели вариации.
Вычисление вариации
Вариация непрерывно дифференцируемой функции
Если функция 
принадлежит классу 
, то есть имеет непрерывную производную первого порядка на отрезке 
, то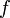 
— функция ограниченной вариации на этом отрезке, а вариация вычисляется по формуле:
то есть равна интегралу нормы производной.
Дата добавления: 2015-08-02; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Экономика | | | Дисперсия невзвешанная Дисперсия взвешанная |