Оформление результатов анализа

Результаты экспериментальных определений дисперсного состава в большинстве случаев представляются в виде таблиц. Наиболее часто данные дисперсионного анализа даются в виде фракций, выраженных в процентах от общего числа или массы измельченного материала или пыли (табл. 1).

Таблица 1. Фракционный состав пыли (пример)

Размеры частиц на границах фракции, мкм	<1,6	1,6–2,5	2,5–4,0	4,3–6,3	6,3–10	10–16	16–25	25–40	>40
Фракции, в % от общей массы частиц	2,08	3,61	8,32	17,56	20,6	18,74	14,57	12,5	2,02

В некоторых методах анализа результаты записывают в виде таблиц с указанием процента массы или числа частиц, имеющих размер либо больше, либо меньше заданного размера (табл. 2).

Таблица 2. Фракции пыли с частицами мельче или крупнее заданного размера (пример)

Размеры частиц d, мкм		1,6	2,5	4,3	6,3					мах
Проход D (мельче d), %	0,00	2,08	5,69	14,01	31,57	52,17	70,91	85,48	97,98	100,0
Остаток R (крупнее d), %	100,0	97,92	94,31	85,99	68,43	47,83	29,09	14,52	2,02	0,00

Содержание частиц мельче и крупнее d можно получить из табл. 1, складывая фракции слева направо и справа налево.

Результаты дисперсионных анализов могут быть изображены графически. При­нимая равномерным распределение частиц по размерам внутри каждой фракции, можно построить ступенчатый график, на­зываемый гистограммой. По оси абсцисс откладываются размеры частиц, а по оси ординат — относительные содержания фрак­ций, т.е. процентное содержание каждой фракции, отнесенное к массе всего мате­риала (рис. 1.1,а).

Если процентное содержание каждой фракции разделить на разность размеров частиц, принятых в качестве граничных, и найденные значения отложить в системе координат, как ординаты точек, абсциссы которых равны среднему для соответству­ющих фракций размеру частиц, то через полученные точки можно провести плав­ную дифференциальную кривую 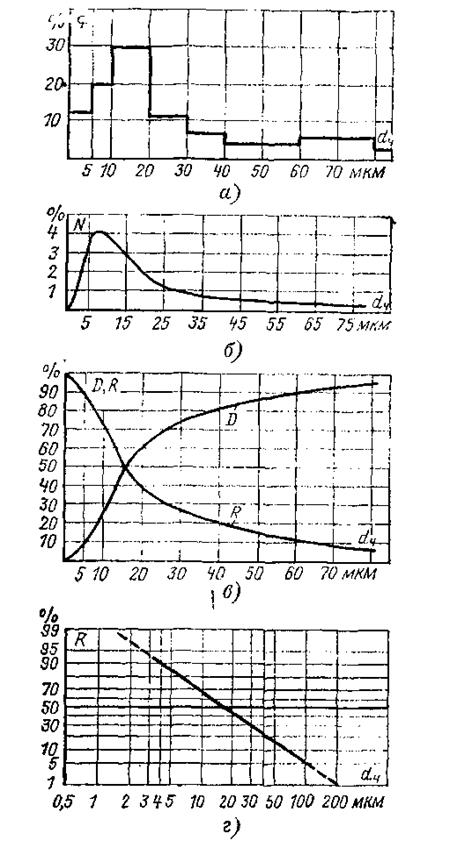распреде­ления частиц по размерам (рис. 1,б).

Рис. 1. Графическое изображение дисперсионного состава пыли (пример): а - гистограмма распределения по фракциям; б – дифференциальная кривая распределения; в – интегральное распределение в линейном масштабе координат; г – интегральное распределение в вероятностно-логарифмической системе координат

Од­нако наиболее удобным является графиче­ское изображение результатов дисперсион­ных анализов в виде интегральных кривых D(d) или R(d), каждая точка которых показывает относительное содержание ча­стиц с размерами больше или меньше дан­ного размера (рис. 1,в).

Интегральные кривые для частиц с логарифмически-нормальным распределением удобно строить в вероятностно-логарифмической системе координат, в которой они приобретают вид прямых линий (рис. 1, г). Для построения такой системы координат по оси абсцисс в выбранном масштабе откладывают десятичные логарифмы значения d, а по оси ординат – значения D(d) или R(d) в относительных длинах отрезков. Относительные длины отрезков, соответствующие различным значениям D(d) или R(d), приведены в табл. 3. Поскольку в вероятностно-логарифмической системе координат ось абсцисс начинается от точки на оси ординат, соответствующей значению 50%, значение Хi для D(d) или R(d) больше 50% откладывается вверх от начала оси абсцисс, а меньше 50% – вниз. Для удобства чтения интегральных кривых в вероятностно-логарифимических координатах вдоль осей вместо значений десятичных логарифмов диаметров частиц и вероятностей их распределения подписываются их абсолютные значения.

Таблица 3. Относительные длины отрезков вероятностно-логарифмической системы координат

R, %	D, %	Относительный масштаб, Хi	R, %	D, %	Относительный масштаб, Хi
		0,000			0,842
		0,050			0,915
		0,100			0,994
		0,151			1,080
		0,202			1,175
		0,253			1,282
		0,305			1,405
		0,358			1,555
		0,412			1,645
		0,468			1,751
		0,524			1,881
		0,583			2,054
		0,643			2,326
		0,706	0,5	99,5	2,576
		0,772	0,3	99,7	2,748

Построив по результатам дисперсионного анализа интегральную функцию распределения частиц по размерам в вероятностно-логарифмической системе координат, можно выразить это распределение в виде двух параметров d_m (d₅₀) – медианного для данного распределения размера частиц (т.е. размера при котором количество частиц крупнее d_m равно количеству частиц мельче d_m) и lgσ_ч – логарифм среднеквадратичного отклонения размеров частиц в функции данного распределения.

Значению d_m отвечает точка пересечения построенного графика с осью абсцисс, а lgσ_ч находят из соотношения, которое является свойством интеграла вероятности функции распределения размеров частиц:

– если строился график функции R(d):

lgσ_ч=lg d_15,9– lg d_m= lg d_m – lg d_84,1,

– если строился график функции D(d):

lgσ_ч= lg d_84,1– lg d_m= lg d_m – lg d_15,9,

Здесь d_84,1 и d_15,9 – абсциссы точек, ординаты которых имеют значения 84,1% и 15,9% соответственно.

В ряде случаев логарифмически-нормальные распределения частиц по размерам оказываются нарушенными или с самого начала не являются таковыми. При этом результаты дисперсионного анализа не будут выражаться прямой линией в вероятностно-логарифмической системе координат. Для подобных случаев имеется целый ряд более общих формул, выражающих функции распределения частиц по размерам.

Параметры d_m и lgσ_ч являются характеристиками дисперсного состава пыли, определяют эффективность сухих пылеуловителей (циклонов, пылеосадительных камер) и используются для их расчета.

---

Дата добавления: 2015-08-02