Основные положения статики

Решение задач статики возможно лишь после того, как хорошо изучены аксиомы статики.

Аксиомы статики — это основные положения, на которых основана теория равновесия. Они устанавливают основные свойства сил, приложенных к телу.

Особое внимание следует обратить на аксиому о равенстве сил действия и противодействия. Эта аксиома рассматривает взаимодействие двух сил. Сила действия приложена к одному телу, а сила противодействия — к другому, поэтому они не могут уравновешиваться, так как эффект действия сил различен для каждого тела. На основании аксиомы о равенстве действия и противодействия опоры тел или, как говорят, их связи, можно заменить силами. Одной из важнейших задач при этом является умение правильно определить направление силы реакции опоры. Для этого нужно внимательно разобраться в устройстве той или иной опоры и схематически изобразить опорные поверхности.

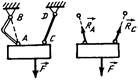
Гибкая нерастяжимая нить (трос, канат, цепь, ремень). Реакции R_A и R_B направлены вдоль нити к точке подвеса (рис. 1.1).

Рис. 1.1. Реакции гибких нитей	Рис. 1.2. Реакции при шарнирном закреплении стержня

Невесомый жесткий стержень. Невесомым называется стержень, массой которого можно пренебречь. Связь выполняется с помощью жесткого стержня, концы которого закреплены шарнирно, например, как стержни АВ и CD на рис. 1.2. Реакции R_A и R_B направлены вдоль прямой, соединяющей центры шарниров.

Гладкая поверхность. Поверхности называют гладкими, если силами трения, возникающими в точках их контакта, можно пренебречь. Реакция R гладкой поверхности или опоры направлена по общей нормали к поверхностям тел в точке их касания и приложена в той же точке (рис. 1.3, а).

Если одна из соприкасающихся поверхностей является точкой, имеет заострение или ребро, то реакция R_A (R_B или R_C) направлена по нормали к другой поверхности (рис.1.3, б).

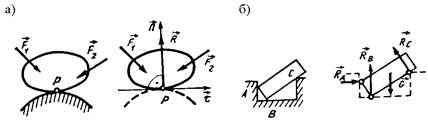
Рис. 1.3. Реакции при свободном опирании тел

Шероховатая поверхность (рис. 1.4). Направление реакции R такой связи заранее неизвестно, поэтому обычно определяют две ее составляющие: нормальную реакцию R_n и касательную — силу трения F_f:

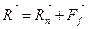. (1.1)

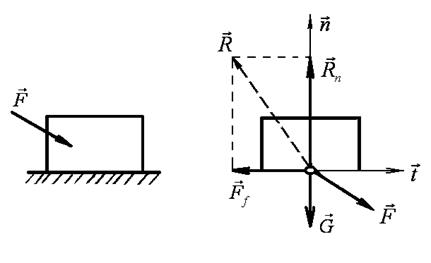
Рис. 1.4. Нормальная реакция R_n шероховатой поверхности и сила трения F_f

Сила трения действует в плоскости, касательной к соприкасающимся поверхностям в точке их контакта, и направлена в сторону, противоположную той, куда активные силы стремятся сдвинуть тело. Сила трения может принимать любые значения от нуля до максимального значения, которое достигается в момент выхода тела из положения равновесия:

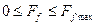. (1.2)

Максимальная сила трения скольжения равна произведению статического коэффициента трения f на нормальную реакцию:

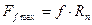. (1.3)

При скольжении одного тела по поверхности другого сила трения направлена в сторону, противоположную направлению движения, и равна произведению динамического коэффициента трения f_v на нормальную реакцию:

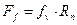. (1.4)

Значения коэффициентов трения для различных материалов приводятся в справочниках.

При практических расчетах рассматривают предельное равновесие тела, когда сила трения равна F_{f max}. При этом уравнения равновесия дополняют равенством (1.3).

Определив реакции связей из уравнений равновесия тела, получают исходные данные, необходимые, например, для расчета элементов конструкции на прочность.

Заделки. Глухая заделка, или жесткое защемление (рис. 1.5, а), исключает любые перемещения тела. Примером такой связи является соединение двух стержней с гарантированным натягом. При действии на балку плоской системы сил в заделке возникают пара сил с реактивным моментом M_A и произвольно направленная реакция R_A с составляющими R_AX и R_AY.

Скользящая заделка (рис. 1.5, б) допускает осевое перемещение стержня, система реакций состоит из силы R_A и пары сил с моментом M_A.

Свободная заделка (рис. 1.5, в) не препятствует перемещениям стержней вдоль своих осей, но исключает возможность их поворота. Поэтому, если не учитывать массу балки, в такой заделке возникает только реактивный момент M_A.

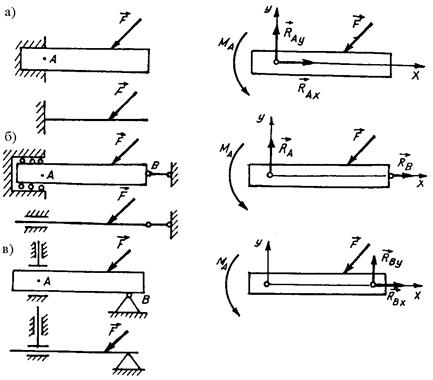
Рис. 1.5. Заделка глухая (а), скользящая, или подвижная (б), свободная (в),
их условные изображения и направления реакций при действии плоской
системы сил

Подвижный шарнир (шарнирно-подвижная опора). Нижняя обойма в опоре А (рис.1.6, а) установлена на цилиндрические катки. Поэтому балка АВ имеет возможность поворачиваться относительно оси шарнира и перемещаться вдоль опорной плоскости катков. Реакция связи R_A направлена перпендикулярно к опорной плоскости катков.

Условные изображения шарнирно-подвижной опоры показаны на рис. 1.6, б.

Рис. 1.6. Шарнирно-подвижная опора:

а – схемы и направления реакций; б – условные изображения

Неподвижный шарнир (шарнирно-неподвижная опора). Такая опора состоит из двух обойм, между которыми расположен цилиндрический стержень. Одна обойма (рис. 1.7, а) закреплена на балке АВ, а другая - на неподвижном основании. Кроме того, шарнирное соединение может выполняться с помощью пальца О, вставленного в цилиндрические отверстия стержня С и опоры D (рис. 1.7, б). Балка АВ и стержень С могут только поворачиваться относительно оси шарнира. Другие перемещения исключены.

Направление реакции связи заранее неизвестно. Реакция связи действует в плоскости, перпендикулярной к оси шарнира. Для неподвижного шарнира она может быть представлена двумя составляющими по координатным осям:

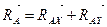. (1.5)

Условные изображения шарнирно-неподвижной опоры показаны на рис. 1.7, в.

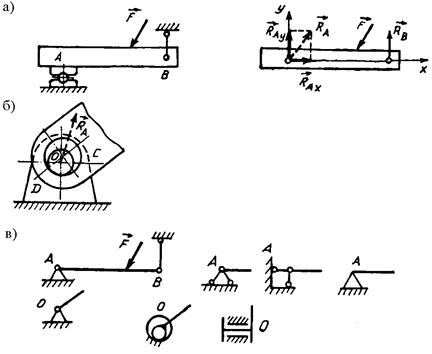
Рис. 1.7. Шарнирно-неподвижная опора:

а, б – схемы и направления реакций; в – условные изображения

Решение задач на равновесие геометрическим методом — построением силовых многоугольников — целесообразно лишь в том случае, если к телу приложено не более трех сил. Более удобным и универсальным методом решения задач на равновесие является аналитический метод. Он основан на составлении и решении уравнений равновесия. Для равновесия плоской системы сходящихся сил достаточно, чтобы алгебраическая сумма проекций сил на каждую ось координат равнялась нулю:

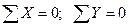. (1.6)

В различных учебниках можно встретить и другие формы записи этих же уравнений. Например:

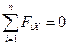и 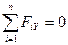. (1.7)

В Международной системе единиц силы измеряются в ньютонах (Н). В ряде учебников и другой технической литературе встречается и другая единица измерения - килограмм-сила (кгс). В этом случае, при необходимости, приходится делать перевод старых единиц измерения в единицы СИ, пользуясь следующими соотношениями: 1кгс=9,81Н; 1тс=9,81кН (1кН=1000Н).

Напоминаем, что проекция силы на ось равна произведению модуля силы на косинус ее острого угла с осью (рис. 1.8). Знак проекции (рис. 1.8) определяется совпадением направлений проекции и оси (направление проекции - от а к b).

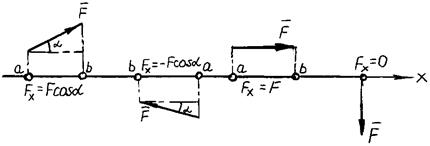
Рис.1.8. Проекция силы на ось

Обращаем внимание на возможность упростить решение подобных задач путем рационального выбора направления координатных осей.

Решив задачу аналитическим методом, следует затем проверить правильность решения:

а) с помощью графоаналитического метода (если система состоит из трех сил);

б) с помощью графического метода (если в системе более трех сил).

Дата добавления: 2015-08-02