Читайте также:
|
Реляционная модель данных является совокупностью взаимосвязанных двумерных таблиц – объектов модели. Связи между двумя логически связанными таблицами в реляционной модели устанавливаются по равенству значений одинаковых атрибутов этих таблиц.
Relation (отношение), т.е. двумерная (реляционная) таблица, обладающая определенными свойствами.
Таблица описывает некоторый информационный объект. Одна строка (запись) хранит 1 экземпляр этого объекта.
Отношение – двумерная таблица, обладающая определенными (5) свойствами.
Определенными свойствами реляционной (двумерной) принято считать:
11) В ячейке хранится атомарное значение (неделимое значение);
12) Все столбцы однородные (один тип данных на столбец);
13) Каждый столбец имеет уникальное имя;
14) Возможна произвольная перестановка, как строк, так и столбцов;
15) В таблице не может быть одинаковых строк.
Атрибут – поименованная характеристика объекта, с помощью которой моделируется его свойства. Атрибут показывает, какая информация должна быть собрана об объекте [объект – клиент банка; атрибут – номер счет, адрес, сумма вклада, ФИО и т.д.]
Кортеж отношения – строка, запись.
Степень(-арность) отношения – количество столбцов таблицы.
Мощность отношения – (количество строк таблицы) – характеристика, обозначающая максимальное количество экземпляров одного объекта, связанных с экземпляром другого объекта.
Домен – совокупность допустимых значений атрибута.
Схема отношения – совокупность заголовков таблиц.
Первичный ключ – минимальный набор атрибутов, который однозначно определяет каждую запись. Свойства ключа: минимальность и уникальность.
Таблица с установленным первичным ключом считается главной таблицей.
Главной таблицей называется такая таблица, которой не требуется другая таблица для полной идентификации её полей.
Зависимая (дочерняя) таблица – такая таблица, которой требуется другая таблица для расшифровки её полей.
Поле в зависимой таблице, которое соединяется с ПК в главной таблице, называется внешним ключом.
Основоположником реляционной модели является английский математик Эдгар Кодд.
Кодд предложил не только реляционную модель, он так же предложил язык обработки данных: реляционную алгебру и реляционное исчисление. И тот, и другой языки построены на математическом аппарате.
Реляционная алгебра – это процедурных язык обработки [реляционных] таблиц. Результат запроса формируется за несколько шагов.
Реляционное исчисление – непроцедурный язык. В реляционном исчислении результат формируется за один шаг.
Для эти языка взаимно эквивалентны.
В последнее время получило распространение реляционное исчисление. SQL (Structured Query Language) – язык структурированных запросов – относят к реляционному исчислению.
Основными операциями реляционной алгебры считают:
| 1. Объединение (Union) | Бинарные операции (операции над двумя таблицами) Для объединения, пересечения и разности важна структура таблиц. | Все кортежи двух отношений (таблиц). Без дубликатов. |
| 2. Пересечение | Результат: только общие кортежи (строки) двух таблиц | |
| 3. Разность | Получаем только те строки, которые принадлежат таблице, из которой вычитают. | |
| 4. Декартово произведение | ||
| 5. Деление | ||
| 6. Соединение (Join) | Симметричное соединение таблиц. Должен быть общий атрибут. | |
| 7. Выборка (Select/селекция) | Унарные операции (т.е. выполняемые над одной таблицей) | Горизонтальный фильтр на таблицу (по строкам) |
| 8. Проекция (Project) | Вертикальный фильтр на таблицу (на столбец) |
1. При объединение двух отношений получаем все кортежи (строки) двух отношений: исхкортежи1 U исхкортежи2 
2. При пересечении двух отношений получаем только общие кортежи этих отношений: исхкортежи1 ∩ исхкортежи2 
3. При выполнении операции разность получаются только те кортежи, которые принадлежат уменьшаемой таблице.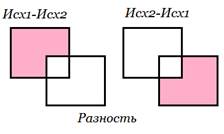 
Исхкортежи1\Исхкортежи2
Даны два отношения R и S.
| R | ||
| A | B | C |
| a | b | c |
| S | ||
| A | B | C |
| d | e | f |
K 1=R U S
K 2= R ∩ S
K 31 = K\S
K 32 = S\K
| K1 | ||
| A | B | C |
| a | b | c |
| d | e | f |
| K2 | ||
| A | B | C |
| K 31 | ||
| A | B | C |
| a | b | c |
| K 32 | ||
| A | B | C |
| d | e | f |
Для операций 1- 3 (объединение, пересечение, разность) важна структура отношений.
4. Декартово произведение
Даны два отношения R и S.
| R | ||
| A | B | C |
| a | b | c |
| M | |
| A | B |
| a | b |
R  M
| ||||
| A | B | C | A1 | B1 |
| a | b | c | ||
| a | b | c | a | b |
| a | b | |||
| a | b |
5. Соединение (операция Join)
Для выполнения соединения таблиц, у таблиц должен быть по крайне мере один общий атрибут. Ко всем (к каждому) кортежам одного отношения добавляется каждый кортеж другого отношения, елси у них значения соединяемого атрибута совпадают.
Симметричное соединение (Inner Join) представляет собой декартово произведение двух отношений, на которым выполнена селекция (выборка) по какому-то условию.
| R | ||
| A | B | C |
| P | a | |
| P | b | |
| Q | e |
| S | |
| D | C |
| a | |
| b | |
| d | |
| b |
R  S по C (т.к. только атрибут С – общий)
| |||
| A | B | C | D |
| P | a | ||
| P | b | ||
| P | b |
6. Деление
7. Выборка (селекция) – горизонтальный фильтр на таблицу по строкам.
8. Проекция – вертикальный фильтр на таблицу по столбцам.
Пример: пусть даны отношения R1 – список абитуриентов, сдававших экзамены по окончанию подготовительных курсов; R2 – список абитуриентов, сдававших экзамены на общих условиях; R3 – список принятых в колледж. Необходимо использую операции над отношениями выполнить задания:
1) Определить список абитуриентов, которые поступали два раза и не поступили. (R1 
R2\R3)
2) Определить поступивших с первого раза. ((R1\R2 ∩ R3) 
(R2\R1 ∩ R3))
3) Определить поступивших со второго раза (R1 R2 ∩ R3)
4) Определить тех, кто поступал один раз и не поступил. ((R1\R2 \ R3) (R2\R1\ R3))
Дата добавления: 2015-08-02; просмотров: 149 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Типы связей в реляционной модели. | | | Целостность данных |