Равномерное приближение функций полиномами

Близость полинома Pn(x,a) к таблично заданной функции f(xk), , можно оценить величиной модуля их разности
		(1)
Если m=n+1, то можно построить полином, обеспечивающий выполнение условия D(xk ,a)=0,k=1,2,..m, т.е. решить задачу интерполирования. При m > n+1 интерполяция нереализуема, но возможно построение полинома Pn(x,a^*), который минимизирует модуль уклонения в узлах сетки, т.е.
		(2)
Такой полином называется полиномом наилучшего равномерного приближения табличной функции. Для m=n+2 задача нахождения полинома наилучшего равномерного приближения получила название задачи чебышевской интерполяции (но интерполирование в обычном смысле здесь невозможно и название отражает лишь историческую реальность). 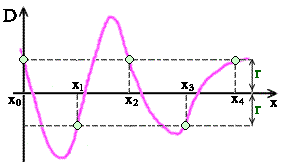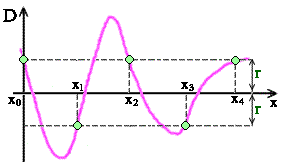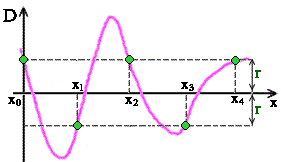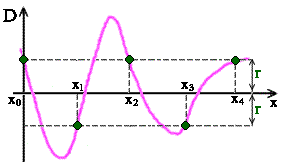Необходимым и достаточным условием построения чебышевского интерполяционного полинома является выполнение условия: D(xk,a)=(-1)^k h, k=1,...,m (3)При этом |h| =r. Таким образом, функция уклонения D(xk ,a) изменяет свой знак при переходе от узла к узлу, но по модулю во всех узлах одинакова. Задача чебышевского интерполирования, не представляя самостоятельного практического интереса, является инструментом решения общей задачинаилучшего равномерного приближенияпри m>n+2. В этом случае проблема сводится к нахождению среди m узлов таблицы такой сетки S^*, состоящей из n+2 узлов, на которой величина уклонения чебышевского интерполяционного полинома м а к с и м а л ь н а, т.е. . Основная трудность построения искомого полинома заключается в разумной организации перебора возможных сеток Si (их общее число, даже при умеренных величинах m, громадно). Одним из наиболее эффективных методов решения этой задачи является R-алгоритм, исследование которого предполагается в ходе численных экспериментов. Построение полинома наилучшего равномерного приближения непрерывной функции f(x), , можно рассматривать как предельный переход в рассмотренной выше дискретной задаче при . К сожалению, нет общих оценок для определения величины m, при которой решения дискретной и непрерывной задач достаточно близки. Можно принять значение mk приемлемым при выполнении условия r(S^*,mk) - r(S^*,mр) <= e, где mk < mр и e - заданная мера точности решения.

Дата добавления: 2015-08-02