Порядок выполнения.

Первый этап - ввод исходных данных:
1. Ввести на рабочем листе необходимые исходные данные и определить их взаимосвязи с результирующими данными:

1.1. Построить таблицы для ввода количества перевозок, цены перевозки и стоимости перевозки из пункта производства “Х” в пункт потребления “Y”, как показано на Рис.1 (количество перевозок для каждого пункта в начале решения задачи будет равно 0).

1.2. Ввести в ячейки С14-G14 потребности складов в товаре, а в ячейки В16-В18 – производственные возможности пунктов производства.

1.3. Ввести в ячейки С16-G18 цены на перевозку товара из пункта производства Х в пункт потребления Y.

2. Ввести формулы в вычисляемые ячейки:

2.1. В ячейки В8:В10 ввести формулы вычисления общего количества перевезенного товара для каждого из пунктов производства (например, формула для ячейки В8=СУММ(С8:G8), т.е. количество перевезенного товара для Белоруссии).

2.2. В ячейки С12:G12 ввести формулы вычисления общего количества перевезенного товара в каждый из пунктов потребления (например, формула для ячейки С12=СУММ(С8:С10), т.е. количество перевезенного товара в Казань).

2.3. В ячейки С20:G22 ввести формулы вычисления общей цены за перевозку товара из каждого пункта производства в каждый пункт потребления, умножив цену перевозки единицы товара (ячейки С16-G18) на общее количество перевезенного товара (ячейки С8-G10) (например, формула для ячейки С20 – общая цена перевозки товара из Белоруссии в Казань – =С8*С16).

2.4. В ячейки С24:G24 ввести формулы вычисления стоимости всех перевозок по каждому из пунктов потребления (например, для Казани в ячейку С24 вводится формула =СУММ(С20:С22)).

2.5. В ячейку В24 ввести формулу подсчета всей стоимости перевозок – результат суммирования значений ячеек С24:G24.

3. Выполнить форматирование ячеек рабочего листа, и выделить ячейки с результатами и изменяемыми данными – синим цветом, а ячейки с исходными данными – красным цветом.

Второй этап – поиск решения:
1. При помощи команды “Сервис” – “Поиск решения…” вызвать диалоговое окно задания данных для решения задачи (Рис.2).

2. Задать целевую ячейку

В качестве целевой ячейки выбрать ячейку (аналогичную ячейке В24 на рис. 1), в которой будет подсчитана общая цена всех перевозок.

По условию задачи целевую ячейку следует установить равной минимальному значению.

Рис. 2. Диалоговое окно ввода данных для решения задачи.

3. Задать изменяемые ячейки

Минимальное значение целевой ячейки будет определяться путем изменения данных в ячейках, задающих объемы перевозок от каждого из пунктов производства к каждому пункту потребления (ячейки C8:G10 на рис. 1).

4. Наложить требования (ограничения), которые будут предъявляться к результатам задачи:

4.1. Количество перевезенных грузов не может превышать производственных возможностей заводов (на рис. 1 значения ячеек B8:B10 должны быть меньше или равны значениям ячеек B16:B18).

4.2. Количество доставляемых грузов должно быть равно потребностям складов (т.е. на рис. 1 значения ячеек C12:G12 должны быть равны значениям ячеек С14:G14).

4.3. Число перевозок не может быть отрицательным и не целым (т.е. на рис. 1 значения ячеек C8:G10 должны быть больше или равны нулю и должны быть целыми).

5. Ввести значения в окно “Поиск решения”. Для ввода значений в диалоговое окно “Поиск решений” можно использовать выделение ячеек и интервалов мышью (при заполнении соответствующих полей ввода). Кроме того, в некоторых случаях удобно пользоваться для определения изменяемых ячеек кнопкой “Предположить” – в этом случае в качестве изменяемых ячеек предлагается использовать все влияющие ячейки для ранее определенной целевой ячейки.

Для ввода ограничений необходимо нажать кнопку “Добавить”.

На экране появится диалоговое окно, показанное на Рис.3.

Рис. 3. Окно ввода ограничений.

При помощи этого диалогового окна ввести ранее заданные ограничения. Для ввода значений в области “Ссылка на ячейку” и “Ограничение” можно также пользоваться возможностями Microsoft Excel по выделению интервалов мышью.

6. Инициировать "Поиск решения"

Решение задачи начинается после нажатия кнопки “Выполнить” в диалоговом окне “Поиск решения”. После того, как вычисления закончатся, открывается диалоговое окно “Результаты поиска решения” (Рис.4), в котором выводится сообщение о том, найдено или нет решение поставленной задачи. Если найденное решение устраивает пользователя, он может сохранить его на рабочем листе, нажав кнопку "ОК".

Можно также сохранить найденное решение в качестве сценария с помощью кнопки “Сохранить сценарий” (обычно так поступают в том случае, когда требуется сохранить результаты нескольких различных решений, полученных при изменении нескольких ограничений).

Рис. 4. Окно “Результаты поиска решения”.

Оптимальное количество поставок, которое приведет к минимизации транспортных расходов в соответствии с заданными исходными данных, представлено в таблице на Рис.5.

Рис.5. Результаты вычислений.

Задание. Автомобили изготавливает 2 завода. 1 завод на складе имеет 32 машин, 2 завод 21 машин. Требуется поставить автомобили в распределительные центры города Миасс – 5 автомобилей, Сатка – 15 автомобилей, Карталы 18 автомобилей.

Стоимость доставки одного автомобиля представлена матрицей

	Миасс	Сатка	Карталы
Завод 1
Завод 2

Определить количество автомобилей, перевозимых из каждого завода в каждый центр распределения, таким образом, чтобы общие транспортные расходы были минимальны

Составить отчет о проделанной работе.

Задание. Выполните самостоятельно, по вариантам.

Пример 1.1. Фабрика выпускает продукцию двух видов: П₁ и П₂. Продукция обоих видов поступает в оптовую продажу. Для производства этой продукции используются три исходных продукта - A, B, C. Максимально возможные суточные запасы этих продуктов составляют 6, 8 и 5 т соответственно вариантам. Расходы сырья A, B, C на 1 тыс. изделий П₁ и П₂ приведены в табл. 1.2, по вариантам.

Изучение рынка сбыта показало, что суточный спрос на изделия П2 никогда не превышает спроса изделия П1 более чем на 1 тыс. шт.

Кроме того, установлено, что спрос на изделия П2 никогда не превышает 2 тыс. шт. в сутки.

Оптовые цены за 1 тыс. шт. изделий равны, соответственно, П1 - 3 тыс. руб., П2 - 2 тыс. руб.

Таблица 1.2

Вариант	Исходный продукт	Расход исходных продуктов на производство 1 тыс. изделий (т.)	Максимально возможный запас (т.)
П1	П2
	A
B
C		0.8
	A
B
C	0,5
	A
B
C	0,
	A		0,4
B
C
	A
B
C	0,6
	A		0,7
B
C
	A
B		0,6
C
	A
B		0,3
C

Необходимо спланировать производство так, чтобы доход от реализации продукции фабрики был максимальным?

Построение математической модели следует начать с идентификации переменных (искомых величин), но так, чтобы после этого целевая функция и ограничения могли быть выражены через соответствующие переменные.

В рассматриваемом примере имеем следующее:

Переменные. Так как нужно максимизировать прибыль, а она зависит от объемов производства каждого вида продукции, то переменными являются:

- суточный объем производства изделия П₁ в тыс. шт.;

- суточный объем производства изделия П₂ в тыс. шт.

Целевая функция. Так как стоимость 1 тыс. изделий П₁ равна 3 тыс. руб., суточный доход от ее продажи составит 3 тыс. руб. Аналогично доход от реализации тыс. шт. П₂ составит 2 тыс. руб. в сутки. При допущении независимости объемов сбыта каждого из изделий общий доход равен сумме двух слагаемых - дохода от продажи изделий П₁ и дохода от продажи изделий П₂.

Обозначив доход (в тыс. руб.) через , можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения и , максимизирующие величину общего дохода:

,

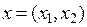
Ограничения. При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов A, B и С и спрос на изготовляемую продукцию, что можно записать так:

Суточный расход исходного продукта для производства обоих видов изделия

Максимально возможный суточный запас данного исходного продукта

Это приводит к трем ограничениям:

+ 2 6 (для А),

2 + 8 (для В),

+ 0.8 5 (для С).

Ограничения на величину спроса на продукцию имеют вид:

- 1 (соотношение величин спроса на изделия П₁ и П₂),

2 (максимальная величина спроса на изделия П₂).

Вводятся также условия неотрицательности переменных, т. е. ограничения на их знак:

0 (объем производства П₁),

0 (объем производства П₂).

Эти ограничения заключаются в том, что объемы производства продукции не могут принимать отрицательных значений.

Следовательно, математическая модель записывается следующим образом.

Определить суточные объемы производства ( и ) изделий П₁ и П₂ в тыс. шт., при которых достигается

при наличии ограничений

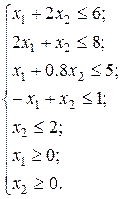
Математическая модель задачи получена. Отметим, что на 3 этапе исследования операций следует выбрать метод решения задачи, для чего её нужно отнести к некоторому классу задач. Полученная модель относится к задачам линейного программирования, так как целевая функция и функции ограничений – линейные, а на переменные наложено ограничение неотрицатльности..

Дата добавления: 2015-08-02