Расчет магнитных цепей. Основным законом, используемым при расчетах магнитных цепей

Основным законом, используемым при расчетах магнитных цепей, является закон полного тока.

(9.1)

Он формулируется следующим образом: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром. Если контур интегрирования охватывает катушку с числом витков W, через которую протекает ток I, то алгебраическая сумма токов 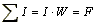, где F - магнитодвижущая сила.

Обычно контур интегрирования выбирают таким образом, чтобы он совпадал с силовой линией магнитного поля, тогда векторное произведение в формуле (9.1) можно заменить произведением скалярных величин H·dl. В практических расчетах интеграл 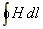заменяют суммой и выбирают отдельные участки магнитной цепи таким образом, чтобы H1, H2,... вдоль этих участков можно было считать приблизительно постоянными. При этом (9.1) переходит в

(9.2)

где l₁, l₂, …, l_n - длины участков магнитной цепи;
H₁·l₁, H₂·l₂ - магнитные напряжения участков цепи. Магнитным сопротивлением участка магнитной цепи называется отношение магнитного напряжения рассматриваемого участка к магнитному потоку в этом участке

,

где S - площадь поперечного сечения участка магнитной цепи,
l - длина участка.

Рассмотрим расчет магнитной цепи, изображенной на рис. 9.2.

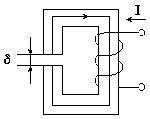Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S.
lср - длина средней силовой линии магнитного поля в магнитопроводе;
δ - толщина воздушного зазора.
На магнитопроводе размещена обмотка, по которой протекает ток I.
Рис. 9.2

Прямая задача расчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу F. Определим магнитную индукцию в магнитопроводе

.

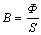По кривой намагничивания найдем значение напряженности магнитного поля H, соответствующее величине В.
Напряженность магнитного поля в воздушном зазоре

.

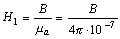Магнитодвижущая сила обмотки

.

При обратной задаче расчета магнитной цепи по заданному значению магнитодвижущей силы требуется определить магнитный поток. Расчет такой задачи выполняется с помощью магнитной характеристики цепи F = f(Ф).
Для построения такой характеристики необходимо задаться несколькими значениями Ф и найти соответствующие значения F. С помощью магнитной характеристики по заданной магнитодвижущей силе определяется магнитный поток.

Дата добавления: 2015-08-02