Читайте также:
|
Рассмотрим величину 
, где 
- число значений первой выборки, относящихся к 
- тому испытанию, 
- число значений второй выборки, относящихся к - тому исходу испытанию. Можно доказать, что при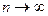 
эта величина сходится к распределению 
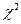с 
степенями свободы. На основании этого строится критерий однородности .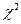
Пример. В двух группах школьников проведены контрольные работы по одним и тем же вариантам.
Таблица 4.2
| Оценка | “2” | “3” | “4” | “5” |
| Первая Группа | человек | человек | человек | человек |
| Вторая Группа | человек | челвека | человек | 6 человек |
.
Здесь 
; 
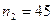. Проверим гипотезы о различии в знаниях учеников первой и второй группы. Установим уровень значимости 
.
: 
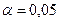- выборки различаются статистическими незначимо;
: 
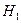- выборки различаются статистическими значимо.
Число степеней свободы 
. По таблице критических точек распределения 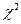с 3-мя степенями свободы найдем критическое значение
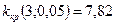. Так как 10,83 > 7,82, то гипотезу отвергаем на уровне значимости 5% и делаем вывод: выборки различаются статистически значимо.
Дата добавления: 2015-08-02; просмотров: 211 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сдачи РГР, контрольных работ, домашних работ, отчетов | | | Кружева в свадебной моде |