Транспортирование разрушенной породы по принципу шнекового транспортера

Транспортирование разрушенной породы осуществляется по принципу шнекового транспортера. Такие транспортеры для перемещения сыпучих материалов известны давно и широко применяются в различных областях техники: в цементной промышленности, на зерновых элеваторах, в сельхозмашинах и в обычной бытовой мясорубке.

Как работает шнековой транспортер при бурении скважины? Шнек состоит из центрального трубчатого стержня, к которому приварена спиральная реборда, представляющая собой винтовую поверхность. При бурении вертикальных скважин элементарный участок винтовой поверхности может быть представлен как наклонная плоскость с углом наклона а, в плане представляющая собой диск (рис. 8.25).

Рис. 8.25. Схема динамики подъема частицы породы при шнековом бурении

Частица породы, отделенная долотом, попадает на спираль шнека и начинает вращаться вместе с ним. За счет вращательного движения на частицу действует центробежная сила, отбрасывающая ее от центра вращения. Поскольку движение частицы по радиусу ограничено стенкой скважины, центробежная сила прижимает частицу к стенке, и со стороны стенки скважины на частицу будет действовать реакция, равная центростремительной силе: F _цс = m Rω², где m — масса частицы; ω—-частота вращения шнека; R — максимальный радиус шнека. На частицу породы также действует сила тяжести G= mg. Вращению частицы вместе со шнеком будет препятствовать сила трения ее о стенку скважины, вызванная центростремительной силой и равная F_с=f_сF_цс, где f_с — коэффициент трения породы о стенку скважины (порода по породе), Под действием силы трения о стенку частица породы частично или полностью удерживается от вращения, а точка шнека, на которой лежала частица, продолжает вращаться, в результате чего возникает относительное перемещение частицы и шнека. Этому перемещению будут препятствовать силы трения частицы о поверхность реборды шнека и составляющая сила тяжести, направленная вниз вдоль спирали (по наклонной плоскости) шнека. Всего сил, действующих вниз вдоль спирали шнека три: составляющая веса F_G=mg sin α, сила трения от нормальной составляющей веса F_шG=fш_mg cos α и сила трения от нормальной составляющей (прижимающей частицу к поверхности шнека), силы трения частицы о стенку скважины F_шс = f_шN_Fc = f_шF_csin α=fшfсmRω².

Вверх по винтовой поверхности шнека действует составляющая частицы о стенку скважины, которую можно назвать подъёмной F_п=F_c cos α =f_cmRω² cosα. Из схемы (рис. 8.26) очевидно, будет двигаться вверх по шнеку, если сила F_п будет больше суммы сил, препятствующих этому движению F_G1 F_шG1, F_шс, т.е. условие транспортирования частицы по шнеку будет составлять

F_п ≥ F_G1 + F_шG1+F_шс (8.16)

Раскрывая выражение (8.16), получим

ƒ_сmRω² cos α ≥ mg sin α + ƒ_ш mg cos α + ƒ_шƒ_с mRω² sinα

и, решив его относительно ω, получим первое условие транспортирования породы при шнековом бурении:

(8.17)

Эта формула действительна для элементарной частицы, расположенной на краю реборды на максимальном удалении от центра вращения, т. е. на расстоянии R. В реальных условиях на реборде одновременно находится значительное число частиц, часть из которых располагается ближе к центру шнека, т. е. их радиус меньше R. Кроме того, поскольку они не касаются стенки скважины, их тормозная сила меньше, чем у частицы, прижатой к стенке.

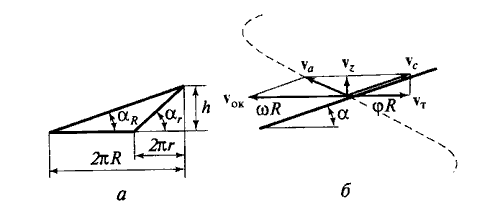
Рис. 8.26. Геометрия витка шнека (а) и кинематика подъема частицы породы при шнековом бурении (6)

Эти обстоятельства учитываются коэффициентами: k₁ = 0,8—0,9 учитывает уменьшение R и k₂ = 0,9 — уменьшение силы трения. Окончательно расчетная формула для подсчета минимально необходимой частоты вращения шнека для подъема породы имеет вид

(8.18)

При использовании этой формулы надо знать свойства и состояние породы, определяющие значения f_c, f_ш, k₁, k₂.. Анализ формулы (8.18) показывает, что для улучшения транспортирования породы шнеком надо стремиться к минимальному значению коэффициент f_ш, для чего поддерживать поверхность реборды чистой, ровной и гладкой. Лучшее транспортирование породы также будет при больших значениях f_c и большем R.

Рассмотрим траекторию частицы породы при ее транспортировании с забоя на поверхность. Винтовая поверхность реборды шнека выполнена таким образом, что угол подъема винтовой линии не одинаков по ширине реборды: больший у стенки центральной трубы шнека и минимальный на внешнем краю реборды. Развертка витка шнека показана на рис. 8.26, а. Здесь h — шаг винтовой спирали шнека; r - радиус трубы шнека; R — наружный радиус реборды шнека; α_r = actg (A/2πr), α_r = arctg (h /2π R). Обычно для буровых шнеков αr-αr = 7—20°. Схема движения частицы породы при ее транспортировании шнеком показана на рис. 8.26, б. Абсолютная скорость движения частицы является векторной суммой вращательного движения частицы со шнеком (переносное движение) и относительного движения (скольжения) частицы по шнеку:

v_a = v_b + v_r

где v_b = ωR — окружная скорость вращательного движения шнека; φR— уменьшение скорости вращательного движения частицы за счет ее торможения трением о стенку скважины. Как видно из схемы, подъем породы обусловлен наличием положительного угла у между абсолютной и переносной скоростями. Значение абсолютной скорости из схемы составляет

v_a = ωR sin α / sin (α + γ) (8.19)

Вертикальная составляющая скорости движения частицы равна

v_z = ωR sin α sin γ / sin (α + γ) (8.20)

Из формулы (8.20) следует, что скорость подъема частицы увеличивается с ростом угла у. Наиболее интенсивный рост вертикальной скорости происходит при значениях угла γ до 15°, а ее максимальное значение будет при γ = 90°, т. е. при полном отсутствии вращения частицы. Однако такого значения γ достигнуть нельзя, поскольку с остановкой вращения исчезнет центробежная сила, прижимающая частицу к стенке скважины. Фактическая траектория движения частицы породы при шнековом бурении представляет собой левую спираль с углом подъема γ.

Вертикальная составляющая, или скорость транспортирования породы определяет возможности шнекового бурения. Если объем породы, получаемой в результате бурения и подаваемой на спираль шнека Q_ш, будет больше транспортирующей способности шнека Q_ш, то произойдёт уплотнение и слипание породы, образование сальника и прекращение транспортировки породы, т. е. создается аварийная ситуация.

Отсюда следует ещё одно условие шнекового бурения: объём разбуриваемой породы должен быть меньше или равен объёму транспортируемой породы, т. е. Q_б≤Q_ш. Из этого соотношения можно определить максимально допустимую скорость бурения:

v_max=(R² - r²) K₁v_z/ (K2K3R²) (8.21)

где К ₁ — коэффициент заполнения шнека породой; К ₂ — коэффициент разбуривания скважины, равный 1,1 — 1,2; К ₃ — коэффициент разрыхления породы, равный 1,2—1,6. Однако воспользоваться этой формулой трудно, поскольку сложно определить вертикальную скорость частицы.

Технические средства для шнекового бурения

Дата добавления: 2015-08-10