Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

(1.3)

,

где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.2) I − I ₁− I ₂=0.

Второй закон Кирхгофа, как одна из форм закона сохранения энергии,

справедлив для любого момента времени, т.е. алгебраическая сумма напря-

жений на всех элементах замкнутого контура электрической цепи в любой

момент времени равна алгебраической сумме ЭДС источников, действую-

щих в контуре:

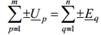
Преобразование схем электр.цепей.
Послед.соединение(рис 18,а)-соединение элементов цепи, в к-ром кажд.элемент соединен не более чем с двумя дрикими,причем так, что с каждым из них у него есть только одна общая точка. Это означает, что в послед.соединение не может быть узлов и во всех элементах протекает один и тот же ток. В соответствие со вторым законом Кирхгофа и законом Ома: , то есть эквивалентное сопротивление m последовательно соединенных резисторов равно сумме их сопротивлений .
Паралл.соед(рис.18,б)-соедиение элементов цепи, в к-ром вс они подключены к одной паре узлов. Это означает, что падение напряжения на все элементах одинаково и равно разности потенциалов узлов. По первому закону Кирхгофа и закону Ома .
Отсюда эквивалентная проводимость паралл.соединения равна .

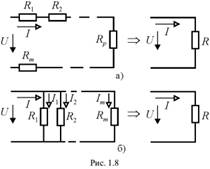
Смешанное соединение –произвольная комбинация послед. и паралл. соединений. Для каждого смешанного соединения можно

найти эквивалентное сопротивление путём последовательных эквивалентных

преобразований отдельных элементов.

Эквивалентное преобразование звезды в треугольник и треугольника в звезду
(смотри в лаб.работе!,но на всякий случай)
Это преобразование часто применяется для упрощения схем электрических цепей. Схемное преобразование показано на рис. 31.

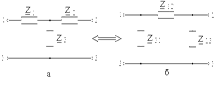
Рис. 31.
Для того, чтобы преобразование было эквивалентным, достаточно равенства сопротивлений между точками 1 – 2, 2 – 3 и 3 – 1 в обеих схемах. Запишем систему уравнений для сопротивлений.
Для точек 1 – 2:
;
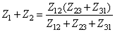Для точек 2 – 3:
;
Для точек 3 – 1:
.
Если решить эту систему относительно сопротивлений Z₁₂, Z₂₃ и Z₃₁ получим формулы преобразования звезды в треугольник.
,
,
.
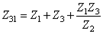Если решить систему исходных уравнений относительно сопротивлений Z₁, Z₂ и Z₃ получим формулы преобразования треугольника в звезду.
,
,
.

Дата добавления: 2015-08-10