Схема Горнера и перевод чисел

Основные понятия систем счисления

Системой счисления или нумерацией называется определенный способ записи чисел. Из Базового курса информатики вы знакомы с историей систем счисления, знаете, что системы счисления бывают позиционными и непозиционными. Вам также известно, что привычная для нас система счисления называется десятичной позиционной системой, что в компьютере для представления чисел и выполнения вычислений используется двоичная система счисления.

Числа заключают в себе количественную информацию. Запись чисел по правилам определенной системы счисления есть способ кодирования чисел. От способа кодирования зависит размер кода, т.е. количество цифр в записи числа, а также правила выполнения вычислений. Одной из главных проблем, которую нужно было решить изобретателям ЭВМ, это проблема представления чисел в памяти компьютера и алгоритма их обработки (вычислений) процессором. Для понимания того, как были решены эти проблемы нужно знать принципы организации систем счисления.

Основные понятия позиционных систем счисления

Цифра – символ, используемый для записи чисел.

Алфавит системы счисления – совокупность всех цифр.

Размерность алфавита – количество цифр в алфавите.

В записи многозначного числа цифры, стоящие в разных позициях, имеют разный вес. Так в целом десятичном числе 325 тройка означает три сотни, двойка – два десятка, пятерка - пять единиц: 325=3·100 + 2·10 +5·1. Такая запись называется развернутой формой записи числа: число записывается в виде суммы, в которой каждое слагаемое – это цифра, умноженная на свой вес. Вот еще пример развернутой записи смешанного десятичного числа:

6248,547 = 6·1000 + 2·100 + 4·10 + 8·1 + 5·0,1 + 4·0,01 + 7·0,001= 6·10³ + 2·10² + 4·10¹ + 8·10⁰ + 5·10^-1 + 4·10^-2 + 7·1^-3

В десятичной системе счисления веса равны степеням десятки (положительным и отрицательным). Каждая позиция в записи числа называется разрядом числа. Разряды нумеруются в целой части числа положительными целыми числами, начиная от нуля, в дробной части – отрицательными числами, начиная от минус единицы:

разряды: 3 2 1 0 -1-2-3

число: 6248,547

Здесь номера разрядов указаны маленькими цифрами сверху. Отсюда видно, что веса соответствующих цифр равны десяти в степени, равной номеру разряда, в котором стоит эта цифра.

Следующий, бесконечный в обе стороны ряд целых степеней десятки называется базисом десятичной системы счисления:

… 10⁹, 10⁸, 10⁷, 10⁶, 10⁵, 10⁴, 10³, 10², 10¹, 10⁰, 10^-1, 10^-2, 10^-3, …

Запись числа в развернутой форме еще называют разложением числа по базису.

Десятичная система относится к числу традиционных систем счисления. Для традиционных систем счисления принято размерность алфавита называть основанием системы счисления. Основание десятичной системы счисления равно десяти.

По такому же принципу организованы все другие традиционные системы счисления. Наименьшим основанием для позиционной системы является 2 – двоичная система. Система с основание 1 не может быть позиционной, поскольку для нее невозможно построить базис - единица в любой степени равна единице. Базис двоичной системы счисления выглядит так:

… 2⁹, 2⁸, 2⁷, 2⁶, 2⁵, 2⁴, 2³, 2², 2¹, 2⁰, 2^-1, 2^-2, 2^-3, …

Основанием традиционной позиционной системы может быть любое натуральное число, начиная от двух, а базис – бесконечный в обе стороны ряд целых степеней основания

Вот несколько примеров позиционных систем и их алфавитов:

Основание	Название	Алфавит
	Двоичная	0 1
	Троичная	0 1 2
	Восьмеричная	0 1 2 3 4 5 6 7
	Шестнадцатеричная	0 1 2 3 4 5 6 7 8 9 A B C D E F

Если n – основание системы не большее десяти, то в алфавите используются n первых арабских цифр. Если основание превышает 10, то в качестве дополнительных цифр выступают буквы латинского алфавита по порядку.

При записи недесятичного числа принято указывать его основание маленькой подстрочной цифрой – нижним индексом. Например: 137₅ – число в пятеричной системе счисления. Отметим одно очень важное обстоятельство:

в любой позиционной системе счисления ее основание записывается как 10.

Например: 10₂=2, 10₃=3, 10₈=8, 10₁₆=16 и т.д.

Задача 1. Число в троичной системе счисления: 2011,1₃ нужно перевести в десятичную систему.

Разложим данное число по базису троичной системы счисления, т.е. запишем его в развернутой форме и вычислим полученное выражение по правилам десятичной арифметики:

2011,1₃= 2·3³+0·3²+1·3¹+1·3⁰+1·3^-1=54+3+1+1/3=

Задача 2. Шестнадцатеричное число 2AF,8C₁₆ перевести в десятичную систему.

Задача также решается через разложение шестнадцатеричного числа по базису системы счисления и вычисления полученного выражения. В разложении цифры, обозначаемые буквами, заменяются на их эквиваленты в десятичной системе.

2AF,8C₁₆=2·16²+10·16+15·16⁰+8·16^-1+12·16^-2=512+160+15+1/2+3/64= 687,546875

Задача 3. Двоичное число 1010101111,100011₂ перевести в десятичную систему.

1010101111,100011₂=1·2⁹+1·2⁷+1·2⁵+1·2³+1·2²+1·2+1+1·2^-1+1·2^-5+1·2^-6= 512 + 128 + 32 + 8 + 4 +2 + 1 +1/2 + 1/32 +1/64 =687,546875.

Обратите внимание, что результат тот же, что и в задаче 2. Значит двоичное число из данной задачи равно шестнадцатеричному числу из задачи 2. К этому обстоятельству мы еще вернемся.

Схема Горнера и перевод чисел

Недесятичное число можно быстро перевести в десятичную систему и с помощью простого калькулятора. Такой перевод связан с применением так называемой схемы Горнера для вычисления алгебраических многочленов. Сначала рассмотрим перевод целого числа на примере восьмеричного числа 231745₈. Запишем его в развернутой форме и преобразуем полученную сумму к эквивалентной скобочной форме:

231745₈ = 2·8⁵+3·8⁴+1·8³+7·8²+4·8+5=((((2·8+3)·8+1)·8+7)·8+4)·8+5=78821

Раскройте мысленно скобки в записанном выражении, и вы увидите, что получится то же разложение по базису восьмеричной системы счисления. Но зато скобочное выражение очень просто вычислять. На калькуляторе нужно последовательно слева направо выполнять умножения и сложения. Порядок нажатия клавиш на калькуляторе будет таким:

×

+

×

+

×

+

×

+

×

+

=

В калькуляторе реализуется алгоритм последовательного выполнения цепочки операций: при нажатии клавиши со знаком операции выполняется предыдущая операция и ее результат высвечивается на индикаторе. После нажатия клавиши «равно» выполняется последняя операция цепочки и на индикаторе отражается результат вычисления всего выражения. В рассмотренном примере было выполнено пять умножений и пять сложений. Такой способ вычисления называется схемой Горнера.

В общем виде алгебраический многочлен n -й степени и его преобразование к скобочной форме выглядит так:

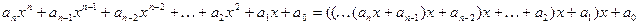
Из этой формулы следует, что алгебраический многочлен n -й степени можно вычислит за n операций умножения и n операций сложения. Это самый оптимальный способ вычисления.

Схему Горнера можно применить и для перевода дробных чисел. Покажем на примере двоичного числа 0,110101₂. Запишем число в развернутой форме и выполним тождественные преобразования, приводящие выражение к скобочной форме:

0,110101₂ = 1·2^-1+1·2^-2+0·2^-3+1·2^-4+0·2^-5+1·2^-6 = 1·2^-6+0·2^-5+1·2^-4+0·2^-3+1·2^-2+1·2^-1 =

=(((((1/2+0)/2+1)/2+0)/2+1)/2+1)/2= 0, 828125

Полученное выражение также поддается последовательному вычислению на калькуляторе: шесть операций деления и пять – сложения. Клавиши нажимаются в таком порядке:

/

+

/

+

/

+

/

+

/

+

/

=

Прибавление нулей можно не делать, тогда число операций сложения сократиться до трех:

/

/

+

/

/

+

/

+

/

=

Практическое задание №1

Выполните быстрый перевод в десятичную систему счисления следующих недесятичных чисел, пользуясь калькулятором и вычислительной схемой Горнера:

а) 3204₅, 1101011₂, 56721₈, 9A3CEF₁₆;

б) 0,3204₅, 0,1101011₂, 0,56721₈, 0,9A3CEF₁₆;

Дата добавления: 2015-08-10