Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Решение задач линейного программирования графическим методом

Читайте также:
  1. I. Задачи маркетингового исследования
  2. I. Постановка задачи. Обсуждение ситуации.
  3. I. Цели и задачи фестиваля.
  4. I. ЦЕЛИ, ЗАДАЧИ, ОРГАНИЗАЦИЯ, ОБЩИЕ ПРИНЦИПЫ И МЕТОДЫ ПРОВЕДЕНИЯ ХИМИЧЕСКОЙ РАЗВЕДКИ
  5. I. Цель и задачи конкурса
  6. II. Задачи практики
  7. II. Основные задачи

Необходимо найти максимальное значение целевой функции F = 3x1-x2 → max, при системе ограничений:

-3x1+2x2≤6 (1)
2x1-3x2≤0 (2)
x1≤6 (3)
x2≤6 (4)
≤0 (5)
x1≥0 (6)
x2≥0 (7)

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение -3x1+2x2 = 6 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 3. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = -2. Соединяем точку (0;3) с (-2;0) прямой линией.
Построим уравнение 2x1-3x2 = 0 по двум точкам. Для нахождения первой точки приравниваем x1 = 1. Находим x2 = 0.67. Для нахождения второй точки приравниваем x2 = 1. Находим x1 = 1.5. Соединяем точку (1;0.67) с (1.5;1) прямой линией.
Построим уравнение x1 = 6. Эта прямая проходит через точку x1 = 6 параллельно оси OX2.
Построим уравнение x2 = 6. Эта прямая проходит через точку x2 = 6 параллельно оси OX1.
Построим уравнение = 0

или

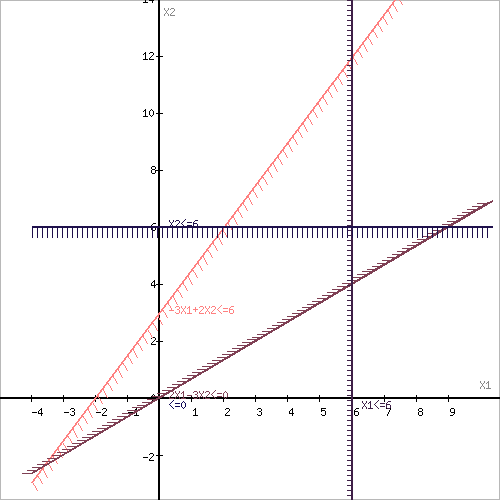
Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.

 

Рассмотрим целевую функцию задачи F = 3x1-x2 → max.
Построим прямую, отвечающую значению функции F = 0: F = 3x1-x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (3; -1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

Равный масштаб

Область допустимых решений представляет собой многоугольник

Прямая F(x) = const пересекает область в точке F. Так как точка F получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
2x1-3x2≤0
x1≤6

Решив систему уравнений, получим: x1 = 6, x2 = 4
Откуда найдем максимальное значение целевой функции:
F(X) = 3*6 - 1*4 = 14

 

Дата добавления: 2015-08-10; просмотров: 123 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Составитель Дэвид Годман| ноября, вторник
mybiblioteka.su - 2015-2024 год. (0.006 сек.)