Читайте также:
|
3.1 Находим приближенное среднее 
и центральные выборочные моменты m 2, m 3, m 4 по формулам
, 
, (e = 2, 3, 4), где 
.
|
| m 2 | m 3 | m 4 |
| 0,3070088 | 1,7022439 | -0,2939567 | 6,7079252 |
Вычисление моментов оформляется в виде таблицы 3.
Таблица 3.
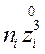
Вычисление выборочных моментов
| N | n(i) | z(i) | n(i)z(i) |
|
|
|
| ||||
| 2,4709375 | -9,88375 | 2,7779463 | 30,867941 | 85,749482 | 238,20745 | ||||||
| 1,7568125 | 10,540875 | 2,0638213 | 25,556149 | 52,743323 | 108,85279 | ||||||
| 1,0426875 | 13,554938 | 1,3496963 | 23,68184 | -31,96329 | 43,140733 | ||||||
| 0,3285625 | 6,2426875 | 0,6355713 | 7,6750655 | 4,8780509 | 3,1003489 | ||||||
| 0,3855625 | 8,0968125 | 0,0785538 | 0,1295845 | 0,0101794 | 0,0007996 | ||||||
| 1,0996875 | 15,395625 | 0,7926788 | 8,7967544 | 6,9730003 | 5,5273492 | ||||||
| 1,8138125 | 27,207188 | 1,5068038 | 34,056863 | 51,317009 | 77,324662 | ||||||
| 2,5279375 | 20,2235 | 2,2209288 | 39,460196 | 87,638284 | 194,63838 | ||||||
| СУММА | 0,0285 | 30,700875 | -2,22807 | 170,22439 | 29,395674 | 670,79252 |
3.2 Вычисляем выборочные среднее квадратическое отклонение S, асимметрию а и эксцесс е по формулам
= 1,3047007
, 
= -0,1323582
= -0,685034
.
Дата добавления: 2015-08-10; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Графические характеристики выборки. | | | Сравнение выборочных графических характеристик с соответствующими теоретическими кривыми нормального распределения. |
