Задачи для допуска к экзамену по ТиТДиПНиГ, 1. ч.

Для определения исходных данных используйте три последних цифры номера своей зачетной книжки(в тексте выделены жирным шрифтом): ABC

C – последняя цифра номера зачетной книжки, в том случае когда C=0 принять в расчетах C =10, аналогично для А и В;

BC – две последние цифры номера зачетной книжки в том случае когда BC =00 принять в расчетах BC =100;

ABC – три последние цифры номера зачетной книжки в том случае когда ABC =000 принять в расчетах ABC =1000.

Задача №1

Определите основные характеристики фиктивного грунта, если размер слагающих его частиц d= ВС´10-2 мм, при 0≤С≤3 угол укладки Θ=70º, при 4≤С≤6 угол укладки Θ=78º, при 7≤С≤9 угол укладки Θ=85º. Число Кармана принять равным 5.

Задача №2

Постройте кривую весового участия фракций и определите эффективный диаметр методом 10%.

Размер частиц, мм	0,0…0,03	0,03…0,1	0,1…0,2	0,2…0,4	0,4…0,9	0,9…2
Количество частиц	BC´1000	С´900	B´300	ABC	BC	С

Задача №3

Определите эффективный диаметр методом веса средней частицы.

Размер частиц, мм	0,0…0,07	0,07…0,12	0,12…0,2	0,2…0,4	0,4…0,9	0,9…2
Количество частиц	BC´2000	B´400	С´300	BC	C

Задача №4

Определите основные характеристики идеального грунта, если размер его капилляров d= BC ´10^{-3 мм, размер ячейки а=} C ´10^{-1 мм.}

Задача №5

Жидкость с вязкостью и плотностью 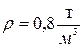под действием собственного веса течет через горизонтальный фильтр диаметром D=55 мм и длинной l = С ´10^-1 м. Фильтрующим материалом является идеальный грунт с диаметром капилляров d= C ´10^{-2 мм и периодом (размером ячейки)} a= В ´10^{-1 мм.}

Уровень жидкости над фильтром H=0.7 м, поддерживается постоянным.

Определите секундный и суточный расходы жидкости через фильтр.

Задача №6

Жидкость с вязкостью и плотностью под действием собственного веса течет через вертикальный фильтр диаметром D=55 мм и длинной l =0,5 м. Фильтрующим материалом является идеальный грунт с диаметром капилляров d= B ´10^{-2 мм и периодом (размером ячейки)} a= C ´10^{-1 мм.}

Уровень жидкости над фильтром H= С ´10^-1 м, поддерживается постоянным. Определите секундный и суточный расходы жидкости через фильтр.

Задача №7

Жидкость с вязкостью и плотностью 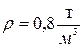под действием собственного веса течет через горизонтальный фильтр диаметром D=55 мм и длинной l = С ´10^-1 м. Расход жидкости через фильтр составил Q= В л/cут.

Уровень жидкости над фильтром H=0.7 м, поддерживается постоянным. Определите проницаемость грунта.

Задача №8

Определите по формуле Щелкачева характер течения флюида в пласте с параметрами m=0,2+ С ´10^-2; проницаемостью k=10^{-12 м2}. Течение в пласте считать прямолинейно-параллельным, при этом площадь поперечного сечения пласта составляет B км², дебет 1000 м³/сут. Кинематическая вязкость флюида 75·10^-6 м²/с, плотность флюида составляет 770 кг/м³. Re_кр=0,05. расстояние до контура питания l=1000м.

Задача № 9

При радиусе скважины r_c1 =50 мм дебет скважины составил Q= С ´10² м³/сут.

Определите по формуле Щелкачева характер течения флюида в пласте с пористостью m=0,2+ В ´10^-2 на радиусах r₁ =700 мм, r₂ =20 м. Поток считать плоскорадиальным. Радиус контура питания составляет R_к=1000 м, давление на контуре питания 230 атм, толщина пласта h=40 м, давление в забое скважины поддерживается постоянным и составляет 190 атм. Вязкость флюида μ =2 Па·с, плотность флюида составляет 720 кг/м³. Re_кр=0,05.

Задача №10

Определите запас нефти в несжимаемом пласте площадью С ´10³ км² и толщиной Δh=75 м. Плотность нефти при атмосферном давлении ρ= 800 кг/м³, пористость пласта m=0,18, коэффициент нефтеотдачи η = 0,7. Пластовое давление составляет 60 МПа. Считать газонасыщение равным 0. Модуль упругости нефти составляет 1200 МПа. Падение пластового вследствие добычи считать значительным.

Задача №11

Определите запас нефти в упругом пласте площадью 30000 км² и толщиной Δh= B м, пористость пласта m=0,2+ С ´10^-2, глубина залегания пласта h = 2800м. Плотность пород слагающих верхние слои ρ_пород=2,2 кг/дм³, эффективное напряжение в скелете σ_эф =15 МПа. Считать газонасыщение равным 0. Плотность нефти при атмосферном давлении ρ= 800 кг/м³, сжимаемость нефти β _ж=20·10^-10 Па^-1. Коэффициент упругости пласта = 2·10^-10 Па^-1. Падение пластового вследствие добычи считать значительным.

Задача №12

Определите коэффициент нефтеотдачи пласта в эксплуатируемого в чистом упругом режиме площадью 700 км² и толщиной Δh= С м, пористость пласта m=0,2+ В ´10^-2, глубина залегания пласта h = 3200м. Плотность пород слагающих верхние слои ρ_пород=2,2 кг/дм³, эффективное напряжение в скелете σ_эф =9 МПа. Считать газонасыщение равным 0. Плотность нефти при атмосферном давлении ρ= 800 кг/м³, сжимаемость нефти β _ж=16·10^-10 Па^-1. Коэффициент упругости пласта = 2·10^-10 Па^-1. Падение пластового вследствие добычи считать незначительным.

Задача №13

Жидкость с вязкостью и плотностью под действием собственного веса течет через горизонтальный фильтр диаметром D=75 мм и длинной l = B м. Фильтр сложен из ша ров диаметром d= C ´10^-1 мм, пористость грунта m=0.259, число Кармана с=5. Уровень жидкости над фильтром H=0.5 м, поддерживается постоянным. Определите секундный и суточный расход жидкости через фильтр.

Задача №14

Определите скорость фильтрации и скорость движения флюида к скважине через пласт шириной B=300 м, толщиной h= C м. Проницаемость пласта k=0,4·10^{-12 м2}, давление в забое скважины p_с=180 атм, давление на контуре питания p_к=210 атм. Расстояние от батареи скважин до контура питания L= BC ´100 м. Просветность пласта s=20%, а вязкость пластовой жидкости ,

Течение в пласте считать прямолинейно-параллельным.

Задача №15

Определите проницаемость пласта с поперечным сечением C км², толщиной h= B м если давление на контуре питания составляет 32 МПа, давление в скважине 26 МПа, вязкость пластовой жидкости , суммарный дебет батареи скважин Q=1200 м³/сут, расстояние от батареи скважин до контура питания R= BC ´100 м, радиус скважины составляет 50 мм. Течение в пласте считать плоскорадиальным.

Задача №16

Определите скорость фильтрации и скорость движения флюида к скважине на расстоянии B ´100 м от неё. Толщина пласта h=20 м. Дебет скважины C ´100 м³/сут. Просветность пласта s=20%. Течение в пласте считать плоскорадиальным.

Задача №17

Определите секундный и суточный дебеты скважины при радиально-сферической фильтрации, если радиус скважины составляет 50 мм, давление на забое скважины 240 атм, радиус контура питания 200 м, давление на контуре питания 276 атм, проницаемость пласта k= C ´10^{-13 м2}. Вязкость флюида μ = B Па·с.

Задача №18

При радиусе скважины r_c1 =50 мм дебет скважины составил Q= BC ´10 м³/сут.

Для увеличения добычи было произведено разбуривание забойной части скважины до r_c2 =150 мм. Определите дебет скважины после разбуривания. Поток считать радиально-сферическим. Радиус контура питания составляет R_к=100 м, давление на контуре питания 200 атм, толщина пласта h=200 м, давление в забое скважины поддерживается постоянным и составляет 190 атм. Вязкость флюида μ = B Па·с.

Задача №19

При радиусе скважины r_c1 =50 мм дебет скважины составил Q= BC ´10 м³/сут.

Для увеличения добычи было произведено разбуривание забойной части скважины до r_c2 =150 мм. Определите дебет скважины после разбуривания. Поток считать плоскорадиальным. Радиус контура питания составляет R_к=190 м, давление на контуре питания 200 атм, толщина пласта h=200 м, давление на забое скважины поддерживается постоянным и составляет 180 атм. Вязкость флюида μ = B Па·с.

Задача №20

Радиус скважины r_c =72 мм, Поток считать плоскорадиальным. Радиус контура питания составляет R_к=1,9 км, давление на контуре питания 230 атм, толщина пласта h=4 м, давление в забое скважины поддерживается постоянным и составляет 190 атм. Вязкость флюида μ =2 Па·с. Грунт пласта эквивалентен фиктивному с параметрами: диаметр частиц d= АВ´10-2 мм, при 0≤С≤3 угол укладки Θ=67º, при 4≤С≤6 угол укладки Θ=72º, при 7≤С≤9 угол укладки Θ=77º. Число Кармана принять равным 5. Определите секундный и суточный дебеты скважины.

Дата добавления: 2015-08-10