
Читайте также:
|
Задача 8. Рассчитать необходимое число опытных долот для получения достоверных и надежных результатов в процессе их испытания при следующих условиях: в данном стратиграфическом подразделении отработаны семь серийно выпускаемых долот. Проходка на долото составляет 25; 23; 23; 24; 27; 29; 37 м.
Решение. Ранжируем величины проходок (от минимальной до максимальной): 23; 23; 24; 25; 27; 29; 37 м.
Проверяем не являются ли две минимальные (23; 23 м) или максимальная (37 м) проходки дефектными. Для исключения явно дефектных данных проверяем максимальные и минимальные величины каждой статистической совокупности следующим образом.
Для исключения максимального значения величины проходки данного ряда необходимо условие
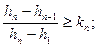 (5)
(5)
минимального значения
 (6)
(6)
Для исключения двух максимальных значений величины проходки данного ряда необходимо условие
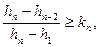 (7)
(7)
двух минимальных значений
 (8)
(8)
Для исключения минимального значения члена ряда в предположении, что и минимальное значение дефектное, необходимо условие
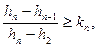 (9)
(9)
Для исключения минимального значения члена ряда в предположении, что и максимальное значение дефектное, необходимо условие
 (10)
(10)
Значение величин, входящих в эти формулы:  -минимальный (первый) член совокупности чисел;
-минимальный (первый) член совокупности чисел;  - соответственно второй, третий, предпоследний и последний (максимальный) член ряда.
- соответственно второй, третий, предпоследний и последний (максимальный) член ряда.
Величину  можно определить по табл. 18 при заданной доверительной вероятности
можно определить по табл. 18 при заданной доверительной вероятности 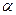 , исходя из числа членов данного ряда
, исходя из числа членов данного ряда  .
.
В нашем случае проверяем, не являются ли две минимальные (23; 23 м) или максимальная (37 м) проходки дефектными.
Т а б л и ц а 18
| Число членов в совокупности |  при доверительной вероятности при доверительной вероятности
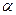 = 0,95 для условий = 0,95 для условий
| ||
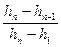 ; ;  ; ;
|  
|  
| |
| 0,941 0,765 0,642 0,560 0,507 0,468 0,437 0,412 0,392 0,376 0,338 0,300 0,281 0,260 | 1,000 0,955 0,807 0,689 0,610 0,554 0,512 0,477 0,450 0,428 0,381 0,334 0,309 0,283 | 1,000 0,967 0,845 0,736 0,661 0,607 0,565 0,531 0,504 0,481 0,430 0,372 0,347 0,322 |
По формуле (8) находим
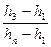 =
=  .
.
По табл. 18 для n = 7 находим  . Так как 0,071<0,0661, то минимальная величина проходки не является дефектной.
. Так как 0,071<0,0661, то минимальная величина проходки не является дефектной.
По формуле (5)
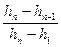

По табл. 18. для n = 6 находим  . Так как 0,167<0,736, то минимальные значения величины проходки не являются дефектными.
. Так как 0,167<0,736, то минимальные значения величины проходки не являются дефектными.
По формуле (5)
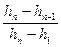
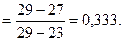
По табл. 18 дл n = 6 находим 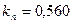 . Так как 0,333<0,560, то максимальная величина проходки нового ряда (29 м) не является дефектной; значит, ряд сохраняется.
. Так как 0,333<0,560, то максимальная величина проходки нового ряда (29 м) не является дефектной; значит, ряд сохраняется.
Определяем среднюю проходку на долото
 м.
м.
Определяем среднее квадратическое отклонение от средней арифметической величины по формуле
 (11) где
(11) где  - размах варьирования величин после исключения явно дефектных данных;
- размах варьирования величин после исключения явно дефектных данных;  - величина, определяемая по табл.19 в зависимости от числа членов ряда.
- величина, определяемая по табл.19 в зависимости от числа членов ряда.
Т а б л и ц а 19
| Число членов ряда после исключения дефектных данных |

| Число членов ряда после исключения дефектных данных |

|
| 1,128 1,693 2,059 2,326 2,534 2,704 2,847 2,970 3,078 | 3,173 3,258 3,336 3,407 3,472 3,532 3,588 3,640 3,689 3,735 |
По формуле (11) находим
 .
.
Определяем выборочный коэффициент вариации по формуле
 (12)
(12)
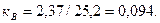
Задаемся предельно допускаемой относительной погрешностью (для шарошечных долот  ); при испытаниях
); при испытаниях  и
и  .
.
При  определяем величину
определяем величину 

При 

По табл. 20 приводится минимальное требуемое число опытных и серийных шарошечных долот сравниваемых конструкций
Т а б л и ц а 20

| 
| 
| 
| 
| 
|
| 1,15 1,00 0,89 0,816 0,754 0,706 0,663 0,630 0,597 0,572 0,550 0,530 0,512 0,495 0,479 0,466 0,454 0,442 0,431 0,421 | 0,412 0,403 0,394 0,387 0,380 0,372 0,366 0,360 0,354 0,349 0,344 0,338 0,333 0,329 0,324 0,320 0,316 0,312 0,308 0,304 | 0,300 0,297 0,294 0,290 0,287 0,284 0,270 0,258 0,248 0,238 0,230 0,222 0,,209 0,198 0,181 0,161 0,139 0,124 0,114 0,098 |
для конкретной характерной пачки пород. Значение величины  даны при
даны при 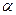 =0,95.
=0,95.
По табл. 20 для  = 3,191 находим
= 3,191 находим 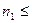 5; для
5; для  = 2,128
= 2,128 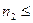 5 долот.
5 долот.
П р и м е ч а н и е. Если в процессе испытаний запланированное число долот обеспечивает величину коэффициента вариации экспериментальных данных  , то результаты проведенных испытаний достоверны и удовлетворительны.
, то результаты проведенных испытаний достоверны и удовлетворительны.
Дата добавления: 2015-08-10; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ИЗ ПРОМЫВОЧНЫХ И СМЕННЫХ НАСАДОК ДОЛОТА | | | ДАННОГО ТИПА |