Тепловые процессы в материалах при действии ЛИ

Знание тепловых процессов позволяет:

1. производить расчет и определять режимы ЛПО, проводить их оптимизацию;

2. прогнозировать структурно-фазовые превращения в поверхностных слоях;

3. оценивать напряженно-деформированные состояния отдельных участков и изделий в целом (остаточные напряжения, остаточные деформации).

На тепловые процессы в материалах оказывает влияние:

1. параметры ЛИ (мощность Р, энергия Е, длительность τ, диаметр пятна фокусирования d0, t(V));

2. обрабатываемый материал:

· поглощающая способность А(Т) – нелинейность II-го рода;

· теплофизические свойства а(Т), с(Т), k(Т) – температуропроводность, теплоемкость, теплопроводность – нелинейность I-го рода;

· размеры и форма – тонкая пластина , полубесконечный массив , изделие клиновидной формы – размер соизмерим с размерами теплового источника, больше и меньше;

Тепловой источник эквивалентный действию лазерного луча при ПО металлических материалов является поверхностным и распределенным. Поверхностным потому, что коэффициент поглощения для металлов очень большой α = 105…106 см-1. Распределенный обусловлено тем, что радиус пятна фокусирования ( – глубина ощутимого прогрева). Последнее позволяет распространением тепла в боковых направлениях пренебречь и тепловую задачу решать как одномерную.

Если величина , то такое тело будем называть полубесконечным. Распространение тепла вдоль оси z описывается одномерным дифференциальным уравнением типа:

где Т – температура

z – координата в направлении действия теплового источника

t – текущее значение времени

а – коэффициент температуропроводности, см2/с

k – коэффициент теплопроводности Вт/(г·см2)

q – интенсивность теплового источника

q = A·Wp·φ(t)

Тепловой источник может иметь различное распределение интенсивности:

· цилиндрическое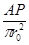

· прямоугольное

· Гауссово

· эллиптическое

· прямоугольное Гауссово

φ(t) – функция, описывающая временную структуру лазерного импульса (прямоугольная φ(t) = 1, треугольная, колоколообразная).

Для решения этого дифференциального уравнения необходимо задать граничные условия 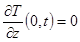, т.е. отсутствует теплообмен с окружающей средой.

Начальными условиями являются:

· Т(∞, t) = Тн – температура на бесконечности за весь период облучения не меняется (равна начальной или нулю);

· Т(z, 0) = Тн – температура в рассматриваемой области в начальный момент времени равна начальной или нулю.

Общим решением уравнения теплопроводности в течении времени t ≤ τ имеет вид:

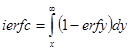
где А – поглощающая способность

τ – длительность импульса

ierfc – функция Бесселя

erfy – функция ошибки

Данные значения табулированы в соответствующих справочниках (например, Лыков "Основы теплопроводности").

Распределение температур на поверхности:

Для учета сдвига критических точек структурно-фазовых превращений (аустенизации) возникает необходимость определения скорости нагрева:

В приведенных зависимостях рассматриваемое время соизмеримо со временем действия ЛИ. В реальных условиях после прекращения действия ЛИ процесс теплопроводности продолжается. Изотерма с фиксированной температурой, например, Тз какое-то время t0 продвигается вглубь материала и достигает максимальной глубины z_max, после чего возвращается к поверхности. Эта z_max представляет практический интерес, поскольку она определяет толщину слоя, в котором протекают соответствующие эффекты (например, закалка).

Для времени t > 0 и больше τ распределение температур описывается зависимостью:

где t₀ – время, за которое заданная изотерма достигает

Из этой зависимости можно определить z_max:

!!!!!!!!!!!!!!!!!!!!!!!

Поскольку t₀ заранее не известно, то рассчитать z_max непосредственно с помощью этого выражения нельзя. Однако его можно аппроксимировать определенными функциями. Если ввести коэффициент b, представляющий отношение искомой изотермы (например, Т_з) к температуре на поверхности 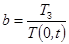, то для различных значений b (для различных материалов сталей) эта аппроксимирующая функция будет иметь различные значения.

Для b < 0,3 (малоуглеродистые стали, эфтектоидные стали) эта зависимость аппроксимируется функцией

0,3 < b < 0,75

0,75 ≤ b ≤ 1 (инструментальные стали)

Определяющей характеристикой структурно-фазовых превращений при закалке является скорость охлаждения, которая может быть определена из зависимости:

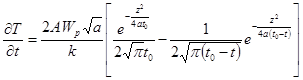
При действии непрерывного ЛИ процессы усложняются, поскольку тепловой источник является движущимся. Считаем, что на полубесконечное тело действует тепловой источник с постоянной интенсивностью:

При этом тепловой источник движется со скоростью V. При этом время действия теплового источника t представляет собой отношение диаметра луча к скорости относительного движения (время, за которое луч проходит свой диаметр):

Для прямоугольного распределения это абсолютно справедливо. Для других распределений, например, Гаусового характерна некоторая ошибка. Усредненное время будет меньше. Распределение температур в этом случае вдоль оси z описывается зависимостью:

(1)

где Ф = 1 – Ф*

В случае, когда глубина прогрева это выражение (1) существенно упрощается:

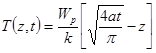
Такое упрощение позволяет рассчитывать температуру с ошибкой не более 10% по отношению к зависимости (1). Чтобы учесть влияние этого упрощения вводится понятие обобщенной скорости:

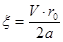
В случае если → 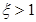, тогда расчет температуры можно вести с помощью упрощенного выражения. Если (или близка) необходимо вводить поправочный коэффициент γ.

γ – поправочный коэффициент представляющий собой отношение безразмерных температур подсчитанных с учетом значений Т1 и Т2 по упрощенной и полной зависимостям

Зная скорость перемещения теплового источника, радиус пятна фокусирования и коэффициент температуропроводности определяется значение ξ, а затем по графику соответственно поправочный коэффициент. Данный поправочный коэффициент вводится на мощность или плотность мощности

С учетом приведенных коэффициентов распределение температур на оси пучка можно записать:

Максимальная глубина проникновения изотермы с температурой не превышающей температуру плавления, но достаточной для закалки будет иметь место в том случае если температура на поверхности материала будет достигать ТПЛ. В этом случае эффективная плотность мощности будет иметь такое выражение:

Максимально достижимая глубина закалки на оси пучка при нагреве без оплавления поверхности может быть определена из двух выражений выше:

Если известна требуемая глубина закалки, а она практически всегда задается чертежом, то, преобразовав последнее выражение, можно найти требуемое время действия теплового источника:

При этом требуемая интенсивность теплового источника:

В соответствии с полученными данными можно определить радиус пятна фокусирования который требуется для обработки на глубину zЗ:

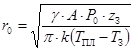
Если известно время и радиус пучка можно определить скорость относительного движения лазерного луча и заготовки:

Поскольку значение поправочного коэффициента γ(ξ) заранее не известно, то расчет режимов проводят двумя способами:

1. метод последовательных приближений – полагают вначале, что γ = 1. Из графика определяют γ(ξ). Пересчитывают режимы с новым значением γ;

2. введение дополнительной функции

F(ξ) можно посчитать используя приведенную зависимость или воспользовавшись графиком. В последнем случае расчет режимов на заданную глубину сводится к определению F(ξ), ξ и γ(ξ), r₀ и V.

Ширина закаленной зоны b_З не всегда соответствует диаметру пятна фокусирования. В зависимости от теплофизических свойств материала, времени облучения и распределения интенсивности она может быть больше или меньше пятна фокусирования. Ее можно определить, воспользовавшись зависимостью:

Обычно ширина закаленной зоны или задается чертежом или выбирается из технологических соображений, т.е. также задается заранее. Поэтому последнюю зависимость удобно применить для нахождения r0.

Значительно реже, но все же возникает задача определения режимов лазерной обработки обеспечивающих максимальную глубину упрочненного слоя.

Изменение температуры на поверхности при z = 0 можно записать в следующем виде:

τ – приведенное время охлаждения

На термокинетической диаграмме (приводятся в соответствующих справочниках) обозначим точку касания критической скорости охлаждения с С-образной кривой Т_i, которая определяет температуру распада аустенита. Из этой диаграммы определяется время охлаждения Δt_i от температуры закалки Т_З до Т_i.

Из кривой охлаждения, представляющей собой зависимость нормированной (отнесенной к ТПЛ) температуры от времени, определяется приведенное время охлаждения Δτi. Зная эти времена можно определить время закалки как отношение

Таким образом, минимальное время t_З, обеспечивающее переохлаждение аустенита до начала мартенситного превращения, является максимальным временем действия лазерного излучения, при котором возможна автозакалка материалов.

Далее по известным зависимостям определяется , затем r₀, V, т.е. все необходимые режимы обработки.

Кроме обработки расфокусированным пучком широко применяется обработка сканирующим пучком.

Дата добавления: 2015-08-10