Рациональные дроби

Рациональнойдробью называется выражение вида

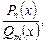(2.7)

где 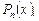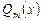– многочлены степени n и m соответственно и

Если для рациональной дроби (2.7) выполняется то дробь называется неправильной, если 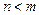– дробь называется правильной.

Среди рациональных дробей выделяют 4 типа простейших дробей:

I.

II.

III. 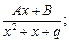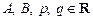и у квадратного трехчлена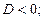

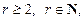
IV. 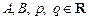и у квадратного трехчлена

Алгоритм разложения дроби (2.7) на простейшие дроби:

1. Если необходимо выделить целую часть делением многочлена 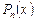на многочлен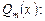

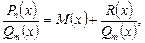
где 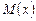– многочлен-частное (целая часть);

– правильная дробь.

2. Разложить 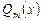на множители:

(2.8)

где

3. Если разложение знаменателя имеет вид (2.8), то дробь можно представить в виде суммы простейших дробей:

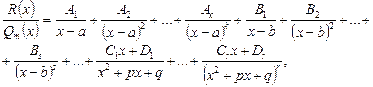(2.9)

где – неопределенные коэффициенты, которые необходимо найти.

4. Для нахождения коэффициентов привести правую часть равенства (2.9) к общему знаменателю, который будет равен знаменателю исходной дроби, т. е.

5. Приравнять числители дробей.

6. Вычислить значения неопределенных коэффициентов и т. д. Для вычисления данных коэффициентов используют следующие методы:

а) метод неопределенных коэффициентов: многочлены в левой и правой части равенства записать в стандартном виде и приравнять коэффициенты при одинаковых степенях числителя;

б) метод частных значений: придать произвольные значения переменной х (удобнее использовать значения 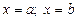и т. д.) и получить равенства для исходных коэффициентов;

в) комбинирование методов а) и б).

7. Подставить полученные числовые значения коэффициентов в равенство (2.9), что и будет искомым разложением.

Пример 1. Разложить на простейшие дроби:

1) 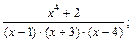2)

3) 4)

5)

Решение. 1) Так как дробь неправильная, выделим целую часть, разделив числитель на знаменатель по правилу деления многочленов. Получим

Для правильной дроби запишем общий вид разложения:

Так как равны знаменатели, то приравниваем числители:

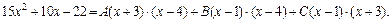
Коэффициенты вычислим методом частных значений. Подставим в последнее выражение последовательно х = 1, х = –3, х = 4.

При 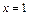получим

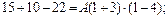
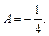
При получим

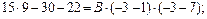
При 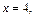получим

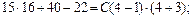
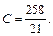
Таким образом,

2) Запишем общий вид разложения на простейшие дроби соответственно виду множителя знаменателя:

Найдем коэффициенты 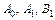методом неопределенных коэффициентов:

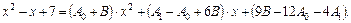
Приравниваем коэффициенты при одинаковых степенях переменной х. Получаем

Пришли к системе уравнений:

Решаем ее:

Таким образом, получаем

или

3) Выделим целую часть дроби так как она неправильная:

Знаменатель полученной правильной дроби разложим на множители и запишем общий вид разложения:

Вычислим коэффициенты, используя метод неопределенных коэффициентов и метод частных значений:

подставим

получим

Запишем многочлен в стандартном виде и используем равенство многочленов:

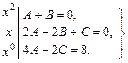
При 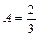система имеет вид:

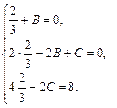
Из нее находим:

Поэтому

4) Разлагаем знаменатель дроби 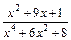на множители:

Записываем общий вид разложения

Приравниваем коэффициенты при одинаковых степенях и решаем систему:

Получаем

5) Знаменатель дроби уже разложен на множители. Записываем общий вид разложения на сумму простейших дробей:

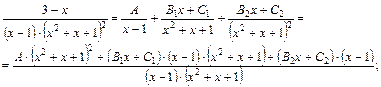
При получаем

Тогда

При система имеет вид:

Поэтому получаем:

Дата добавления: 2015-07-25