Стисла теоретична довідка. У загальному вигляді задача маршрутизації формулюється таким чином: за заданою

У загальному вигляді задача маршрутизації формулюється таким чином: за заданою множиною пунктів виробництва, споживання, розміщення рухомого складу, обсягів поставок та споживання вантажів і обмеженнях на ресурси рухомого складу необхідно визначати припустимі та упорядковані підмножини пов’язаних пунктів (маршрутів), при реалізації яких досягається екстремальне значення цільової функції, що відображає ефективність процесу поставок вантажів.

Задача маршрутизації помашинних відправок виникає у тих випадках, коли у будь-якого відправника кожний окремий автомобіль завантажується (частіше повністю) на адресу тільки одного одержувача. Прикладами таких перевезень є перевезення різноманітних масових вантажів: металопрокат, пісок, щебінь, залізобетонні вироби, лісні матеріали тощо. Маршрутизацію перевезень масових вантажів можна виконувати тільки при наявності груп вантажів, що потребують для перевезення однотипного рухомого складу.

Одним з основних завдань, що виконуються при оперативному плануванні перевезень масових помашинних відправок є оптимізація їх маршрутів з метою підвищення коефіцієнту використання пробігу.

Розглядається сукупність постачальників А ₁, А ₂,…, А_m з обсягами постачання відповідно а ₁, а ₂, …, а_m і споживачів В ₁, В ₂ ,…, В_n з обсягами споживання відповідно b ₁, b ₂, … b_n, що утворюють деяку систему постачання масових вантажів. Обсяг перевезень з і- гопункту відправлення до j- го пункту призначення складає q_ij тонн вантажу. Задана вантажомісткість використовуваних для перевезення автомобілів () та найкоротші відстані між кожною парою пунктів “постачальник”–“одержувач” = .

При виконанні перевезень до пункту доставляється () та відповідно прибуває 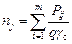завантажених автомобілів, які після розвантаження подаються до пунктів навантаження . Так як з пунктів необхідно вивезти () тонн вантажу, то для пунктів необхідно здійснити відповідно подач порожніх автомобілів.

Нехай – кількість подач порожніх автомобілів від -го пункту розвантаження до -го пункту навантаження. Тоді фактичний порожній пробіг автомобілів складе

. (6.1)

Таким чином, необхідно мінімізувати функцію (порожній пробіг автомобілів) при виконанні умов

; (6.2)

. (6.3)

Сформульована задача є класичною транспортною задачею лінійного програмування. Після попередньої оптимізації порожнього пробігу для складання маршрутів використовують один з методів: таблиць зв’язків чи суміщених планів.

Побудова маршрутів за методом суміщених планів полягає в наступному:

1) відшукують оптимальний план порожніх пробігів, вирішуючи транспортну задачу лінійного програмування з умовами (6.1) – (6.3);

2) у матрицю перевезень у відповідні клітинки записують знайдений план повернення порожніх автомобілів. Таким чином отримують суміщений план;

3) якщо у деякій клітинці матриці присутні значення як завантажених так і порожніх їздок, то така клітинка відповідає маятниковому маршруту зі зворотним порожнім пробігом. Кількість їздок на такому маршруті визначається меншим з двох цифр, що вказують кількість завантажених їздок та подач порожніх автомобілів. Заплановані на маятникових маршрутах перевезення (завезення вантажу та повернення порожніх автомобілів) виключають з матриці;

4) у суміщеному плані будують замкнені чотирьохланкові контури, всі вершини якого лежать у заповнених клітинках, при цьому у вершинах контуру повинні чергуватися завантажені їздки з подачами порожніх автомобілів. Після знаходження такого контуру кількість оборотів на кільцевому маршруті визначається найменшим зі значень, що лежать у вершинах контуру. Маршрут фіксується, а всі значення у вершинах контуру зменшуються на визначену кількість оборотів;

5) після того, як знайдені всі чотирьохланкові контури, у суміщеному плані відшукують шестиланкові, восьмиланкові і так далі доти, доки план перевезень не буде виконано (у матриці не залишиться жодної заповненої клітинки);

6) для кожного маршруту розраховують коефіцієнт використання пробігу. Якщо на деякому кільцевому маршруті він дорівнює b = 0,5, такий маршрут є нераціональним і його розбивають на декілька маятникових.

Дата добавления: 2015-07-20