Скачки уплотнения

ПРЯМОЙ СКАЧОК УПЛОТНЕНИЯ.

Рассмотрим процесс движения ударной волны, когда скачок уплотнения уже сформировался. Допустим, это произошло, как показано на рис.21.1, в момент времени t на расстоянии от поршня х. Скорость движения поршня w, скорость распространения ударной волны u.

Пусть за бесконечно малый промежуток времени dt фронт волны переместился из сечения 1 в сечение 0. Это означает, что в области 1-0 должно наблюдаться увеличение плотности газа на величину 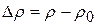. Однако это может произойти только в том случае, если из объема 2-1 в объем 1-0 перетечет некоторое количество газа

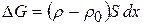. (21.1)

Таким образом, при распространении сильной волны сжатия газ позади волны должен двигаться в том же направлении, что и волна.

Из уравнения неразрывности следует

, (21.2)

откуда с учетом (21.2)

. (21.3)

Но производная пути по времени есть скорость движения волны

. (21.4)

Отсюда имеем

. (21.5)

Применяя к области 1-0 уравнение количества движения, получим

.

Отсюда скорость движения волны сжатия

. (21.6)

Подставляя (21.3) в (21.6), имеем

или

. (21.7)

В случае слабой волны при малом изменении давления и плотности, когда ,

, .

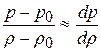Отсюда видно, что слабая волна перемещается со скоростью звука. Так как при сильной волне сжатия , то сильная волна перемещается быстрее скорости звука в невозмущенной среде приблизительно на величину .

Подставляя (21.7) в (21.3), найдем скорость движения газа за ударной волной

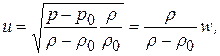
. (21.8)

Вследствие истечения газа из области 2-1 в область 1-0 давление в области 2-1 со временем убывает. Это приводит к тому, что ударная волна, возникшая в неподвижном газе из-за единичного движения поршня или взрыва, всегда затухает. Незатухающая ударная волна существует только в том случае, когда источник возмущения не прекращает своего действия. Например, при движении в газе твердого тела со сверхзвуковой скоростью или при обтекании тела сверхзвуковым потоком перед телом образуется ударная волна постоянной интенсивности.

Движение газа в трубе является нестационарным, так как ударная волна, перемещаясь вдоль трубы, изменяет поле скоростей во времени. Рассмотрим, как показано на рис.21.2, систему координат, двигающуюся вместе с ударной волной.

В этой системе координат фронт ударной волны будет неподвижен, и движение газа станет стационарным. Невозмущенный газ будет подходить к фронту ударной волны справа со сверхзвуковой скоростью w ₁ = - u. После прохождения фронта скорость газа составит w ₂ = w – u.

Примем, что площадь сечения струи газа S = 1. Из уравнения неразрывности следует

.

Изменение количества движения равно величине импульса, действующего на тело. Для единицы времени

или

.

Это выражение можно представить в виде

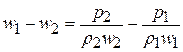. (21.9)

Энтальпия потока определяется выражением

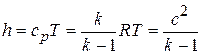. (21.10)

Здесь с - скорость звука при температуре потока Т. Для идеального газа энтальпию можно представить также в виде

. (21.11)

Для заторможенного потока

.

Так как скорость звука в критическом сечении сопла Лаваля

,

то

.

Уравнение Бернулли для газового потока имеет вид

или .

При пересечении потока газа фронта ударной волны в скачке уплотнения происходят необратимые потери энергии, которая рассеивается в виде тепловой энергии. Однако при этом энтальпия газового потока остается неизменной, поэтому также не меняются и температура торможения Т ₀, скорости звука в заторможенном и критическом состоянии с ₀, с _* и температура газа в критическом состоянии Т _*.

Запишем уравнение Бернулли для областей до и после скачка уплотнения:

. (21.12)

. (21.13)

Отсюда

, (21.14)

. (21.15)

Подставим (21.14) и (12.15) в (21.19). Получим

.

Отсюда следует, что 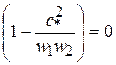или

. (21.20)

Это выражение, полученное Прандтлем, можно представить в безразмерном виде

. (21.21)

Отсюда видно, что при сверхзвуковой скорости до скачка (l ₁ > 1) поток после скачка уплотнения становится дозвуковым (l ₂ < 1).

Можно показать, что изменение полного давления в потоке газа, учитывающее волновое сопротивление, определяется выражением

. (21.22)

График этой зависимости для воздуха показан на рис.21.3.

КОСОЙ СКАЧОК УПЛОТНЕНИЯ

Характерной особенностью прямого скачка уплотнения является то, что, пересекая фронт ударной волны, поток газа не меняет своего направления. При этом фронт волны перпендикулярен направлению скорости газа. Косые скачки уплотнения образуются в том случае, когда фронт волны располагается под некоторым углом к направлению потока. Эта ситуация показана на рис.22.1.

Пусть поток газа подходит к плоскости скачка со скоростью w ₁ под углом . Нормальная составляющая скорости , перпендикулярная фронту волны, скачком снижается до величины w _2n. Тангенциальная составляющая скорости , параллельная фронту волны, остается неизменной . Вследствие того, что полная скорость газового потока , поток поворачивается относительно первоначального направления на угол w. Можно считать, что косой скачок уплотнения сводится к прямому скачку, который сносится вместе с потоком газа вбок во скоростью w_t. В отличие от прямого скачка в косом скачке наблюдается скачкообразное изменение не всей скорости, а только нормальной составляющей.

Для расчета косого скачка вводится понятие температуры частичного торможения, понимая под этим температуру, которую имел бы поток при адиабатическом торможении только нормальной составляющей и неизменной касательно составляющей

. (22.1)

В соответствии с (22.1) вводится также понятие условной критической скорости, соответствующей температуре частичного торможения:

. (22.2)

Формула Прандтля для косого скачка имеет вид

. (22.3)

Полная критическая скорость связана с условной критической скоростью соотношением

. (22.4)

Выражение (22.3) можно представить также в виде

. (22.5)

Для расчета косых скачков используются приведенные скорости газа в виде

. (22.6)

Пользуясь этими величинами, можно получить из (22.3) соотношение

. (22.7)

Изменение статического и полного давлений в косом скачке уплотнения находятся по формулам

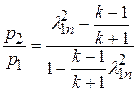, (22.8)

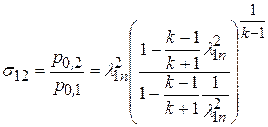. (22.9)

Так как всегда , то при одной и той же скорости набегающего потока косой скачок слабее прямого. Интенсивность косого скачка уплотнения изменяется с изменением угла наклона его фронта к направлению набегающего потока. В предельном случае, когда косой скачок переходит в прямой, увеличение давления получается максимальным. В другом предельном случае, когда угол наклона скачка к направлению потока определяется условием

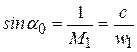, (22.10)

косой скачок вырождается в бесконечно слабую волну.

Дата добавления: 2015-07-21