ЭЛЕКТРОмагнетизм

1. Зависимость пройденного пути S от времени дается уравнением 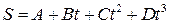, где C = 0,14 м/c² и D = 0,01 м/c³. Через сколько времени после начала движения ускорение тела будет равно 1 м/с². Чему равно среднее ускорение тела за этот промежуток времени.

2. Точка движется вдоль оси ОХ согласно уравнению , где А = 54 см/с, В = 2 см/с³. Определить в какой момент времени точка изменит направление движения.

3. Точка движется по окружности радиусом R = 1,2 м. Уравнение движения точки , где А = 0,5 рад/с; В = 0,2 рад/с³. Определить тангенциальное а_τ, нормальное а_n и полное а ускорение точки в момент времени t = 4 с.

4. По прямой линии движутся две материальные точки согласно уравнениям: и , где А ₁ = 10 м, В ₁ = 1 м, С ₁ = 2 м/с²; А ₂ = 3 м, В ₂ = 2 м/с, С ₂ = 0,2 м/с². В какой момент времени t скорости этих точек будут одинаковы?

5. Точка движется по окружности радиусом R = 2 см. Зависимости пути от времени дается уравнением 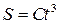, где С = 0,1 м/с³. Найти нормальное и тангенциальное ускорение точки в момент, когда линейная скорость точки v = 0,3м/с.

6. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Закон движения автомобиля . Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды.

7. Маховик спустя 1 мин. после начала вращения приобретает скорость, соответствующую частоте 720 об/мин. Найти угловое ускорение маховика и число оборотов за эту минуту.

8. Точка движется по закону . Определить, в какой момент времени скорость точки обращается в нуль. Найти ускорение точки в этот момент.

9. Определить полное ускорение a в момент времени t = 3 с точки, находящейся на ободе колеса радиусом R = 0.5 м, которое вращается согласно уравнению 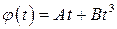, где A = 2 рад/с, B = 0,2 рад/с³.

10. Вентилятор вращается с частотой 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 15 оборотов. Сколько времени прошло с момента выключения вентилятора до полной остановки?

11. Тело массой 2 кг движется прямолинейно со скоростью, зависимость которой от времени . Определить путь, пройденный телом за 5 с, и силу, действующую на тело в конце пятой секунды.

12. Закон прямолинейного движения тела вдоль оси ОХ: 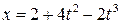. Найти зависимость скорости и ускорения тела от времени и определить их значения в момент времени 2 с.

13. Тело массой m = 2 кг движется с ускорением, изменяющимся по закону . Определить силу, действующую на тело через 5 с после начала движения и его скорость в конце пятой секунды.

14. Велосипедное колесо вращается с частотой 5 об/c. Под действием сил трения оно остановилось за 1 мин. Определить угловое ускорение колеса и число оборотов, которое сделало колесо до остановки.

15. Зависимость пройденного телом пути от времени имеет вид 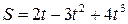. Найти зависимость ускорения тела от времени. Определить, в какой момент времени сила, действующая на тело, равна нулю.

16. Материальная точка движется прямолинейно согласно уравнению , где A = 3 м/с, B = 0,06 м/с³. Найти скорость и ускорение точки в моменты времени t ₁ = 0 и t ₂ = 3 с. Каковы средние значения скорости и ускорения за первые 3 с движения?

17. Материальная точка движется в пространстве согласно уравнениям ; ; 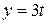. Найти модули радиус-вектора точки, векторов скорости и ускорения точки в момент времени t = 2 с.

18. Материальная точка движется по окружности радиуса R = 20 см равноускоренно с тангенциальным ускорением a_t = 4 см/с². Через какое время после начала движения нормальное ускорение точки будет больше тангенциального в два раза?

19. Материальная точка движется в плоскости ОХY согласно уравнениям 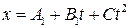и , где В ₁ = 7 м/с; С ₁ = 2 м/с; В ₂ = -1 м/с; С ₂ = 0,2 м/с². Найти модули скорости и ускорения точки в момент времени t = 5 с.

20. Маховое колесо спустя t = 1 мин после начала вращения приобретает скорость, соответствующую n = 720 об/мин. Найти угловое ускорение колеса и число оборотов колеса за эту минуту. Движение считать равноускоренным.

21. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a = 45^о. Пройдя расстояние S = 40 cм тело приобретает скорость v = 2 м/c. Чему равен коэффициент трения тела о плоскость?

22. К саням массой m = 350 кг под углом a = 30^o к горизонту приложена сила F = 500 Н. Определить коэффициент трения полозьев саней о лед, если сани движутся с ускорением a = 0,8 м/с².

23. Подъемный кран поднимает груз массой 1 т. Какова сила натяжения троса в начале подъема, если груз двигается с ускорением 25 м/с²?

24. Груз находится на наклонной плоскости с углом наклона a = 30^o. Коэффициент трения между телом и поверхностью k = 0,15. Определить ускорение груза.

25. Маневровый тепловоз массой 100 т тянет два вагона массой 50 т каждый с ускорением 0,1 м/с². Найти силу тяги тепловоза и силу натяжения сцепок, если коэффициент трения равен 0,006.

26. На наклонной плоскости длинной 15 м и высотой 2 м лежит груз массой 30 кг. Коэффициент трения равен 0,5. Какую силу надо приложить к грузу вдоль плоскости, чтобы втащить груз?

27. Два тела связаны легкой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости. Найти ускорение, с которым будет двигаться тело. Массы тел m = 10 г, М = 20 г, a = 30^о.

28. Тело брошено вертикально вниз с начальной скоростью 2 м/с. Найти потенциальную и кинетическую энергию через 3 сек после броска. Начальная высота тела над поверхностью земли 100 м. Масса тела 0,5 кг. Сопротивлением воздуха пренебречь.

29. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a = 45^о. Пройдя путь S = 36,4 см, тело приобретает скорость v = 2 м/с. Найти коэффициент трения k тела о плоскость.

30. Два тела связаны легкой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости. Найти ускорение, с которым будет двигаться тело. Массы тел m = 10 г, M = 15 г, a =30^о.

31. Уравнение вращения твердого тела j = 3 t ² + t. Определить число оборотов, совершенных телом, угловую скорость и угловое ускорение тела через 10с после начала вращения.

32. На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить, чтобы втаскивать груз вверх с постоянной скоростью.

33. Груз находится на наклонной плоскости с углом наклона a = 30˚. Коэффициент трения между телом и поверхностью k = 0,1. Определить ускорение груза.

34. Две гири массой m ₁ = 2 кг и m ₂ = 1 кг соединены нитью и перекинуты через невесомый блок. Найти: 1) ускорение, с которым движутся гири; 2) натяжение нити. Трением блока пренебречь.

35. Троллейбус массой 10 т, трогаясь с места, приобрел на пути 50 м скорость 10 м/с. Найти коэффициент сопротивления, если сила тяги равна 14 кН.

36. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a = 45˚. Пройдя расстояние S = 36,4 см, тело приобретает скорость v = 2 м/с. Чему равен коэффициент трения тела о плоскость?

37. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a = 45˚. Пройдя расстояние S = 30,5 см, тело приобретает скорость v = 2 м/с. Чему равен коэффициент трения тела о плоскость?

38. К саням массой m = 350 кг приложена сила F = 500 H. Определить коэффициент трения саней о лед, если сани движутся с ускорением а = 0,8 м/с².

39. Тело скользит по наклонной плоскости, составляющей с горизонтом угол 45˚. Зависимость пройденного телом пути от времени дается уравнением S = Ct², где С = 1,73 м/с². Найти коэффициент трения тела о плоскость.

40. Два тела связаны легкой нитью, перекинутой через невесомый блок, установленный на наклонную плоскость. Найти ускорение, с которым будут двигаться тела. Масса тел m = 10 г; М = 15 г; a = 30^о.

41. На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой m ₁ = 6 кг стоит человек массой m ₂ = 60 кг. С какой угловой скоростью w начнет вращаться скамья, если человек поймает летящий на него мяч массой m = 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r = 0,4 м от оси скамьи. Скорость мяча v = 5м/с.

42. На краю платформы в виде диска, вращающегося по инерции вокруг вертикальной оси с частотой n ₁ = 8 об/мин, стоит человек массой m ₁ = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n ₂ = 10 об/мин. Определить массу платформы. Момент инерции человека рассчитывать как для материальной точки.

43. Молотильный барабан вращается с частотой n = 20 с^-1. Момент инерции барабана относительно оси вращения J = 30 кг·м². Определить момент силы относительно оси вращения M, под действием которого барабан остановится за время t = 200 секунд.

44. Человек, стоящий на скамье Жуковского, вращается вместе с нею с угловой скоростью ω = 2 рад/c. Затем он ловит мяч с массой m = 0,5 кг, летящий в горизонтальном направлении на расстоянии R = 1 м от оси вращения скамьи со скоростью v = 20 м/с. Суммарный момент инерции скамьи и человека J = 10 кг∙м². С какой угловой скоростью будет вращаться человек со скамьей, если пойманный мяч ускорил их вращение?

45. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз m = 2 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно, за время t = 3 с приобрел угловую скорость w = 9 рад/с.

46. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой n = 12 с^-1, чтобы он остановился в течение времени t = 8 с. Диаметр блока d = 30 см. Массу блока m = 6 кг считать равномерно распределенной по блоку.

47. К ободу однородного диска радиусом r = 0,2 м приложена постоянная касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения M _тр = 5 Н∙м. Найти массу диска, если он вращается с постоянным угловым ускорением ε = 100 рад/c².

48. Сплошной шар катится по горизонтальной плоскости со скоростью 5 м/с. Определить кинетическую энергию шара, если его масса 2 кг.

49. Маховик, имеющий форму диска массой 30 кг и радиусом 10 см, был раскручен до частоты 300 об/мин. Под действием силы трения диск остановился через 20 с. Найти момент сил трения, считая его постоянным.

50. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m ₁ = 12 кг. На цилиндр намотан шнур, к которому привязана гиря массой m ₂ = 1 кг. С каким ускорением будет опускаться гиря?

51. Маховик (однородный диск) массой 30 кг и радиусом 10 см был раскручен до частоты 400 об/мин. Под действием силы трения диск остановился через 20 с. Найти момент силы трения относительно оси вращения.

52. Горизонтальная платформа массой 70 кг и радиусом 1 м вращается с частотой 30 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от J ₁ = 1,8 кг∙м до J ₂ = 0,8 кг∙м. Считать платформу круглым однородным диском.

53. Человек, стоящий на скамье Жуковского, вращается вместе с ней с угловой скоростью w ₀ = 2 рад/с. Затем он ловит мяч m = 0,5 кг, летящий в горизонтальном направлении на расстоянии R = 1 м от оси вращения скамьи со скоростью v = 20 м/с. Суммарный момент инерции человека и скамьи J = 10 кг∙м². с какой угловой скоростью ω будет вращаться человек со скамьей, если пойманный мяч ускорит их вращение?

54. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой n ₁ = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой n ₂ будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от J ₁ = 2,94 кг∙м² до J ₂ = 0,98 кг∙м². Считать платформу однородным диском.

55. На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Найти момент инерции барабана, если известно, что груз опускается с ускорением а = 2,04 м/с².

56. На барабан радиусом R = 0,5 м намотан шнур, к которому привязан груз массой m = 15 кг. Найти момент инерции барабана, если известно, что груз опускается с ускорением а = 1,5 м/с².

57. На краю платформы в виде диска, вращающегося по инерции вокруг вертикальной оси с частотой n ₁ = 8 1/мин, стоит человек массой m ₁ = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n ₂ = 10 1/мин. Определить массу m платформы. Момент инерции человека рассчитать как для материальной точки.

58. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m ₁ = 12 кг. На цилиндр намотан шнур, к которому привязана гиря массой m = 1 кг. С каким ускорением будет опускаться гиря?

59. Горизонтальная платформа массой 80 кг и радиусом 1 м вращается с частотой 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой будет вращаться платформа, если человек опустив руки, уменьшит свой момент инерции от 2,94 кг∙м² до 0,98 кг∙м². Считать платформу круглым однородным диском.

60. Нить с привязанными к ее концам грузами m ₁ = 50 г и m ₂ = 100 г перекинута через блок диаметром D = 5 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение e = 1,5 рад/с².

61. В баллоне объемом 15 л находится аргон при давлении 600 кПа и темпеpатуpе 300 К. Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до 400 кПа и установилась темпеpатуpа 260 К. Определить массу аргона, взятого из баллона.

62. Определить внутреннюю энергию водорода, а также среднюю кинетическую энергию молекулы этого газа при темпеpатуpе 300 К, если количество вещества водорода равно 0,5 моль.

63. Найти полную кинетическую энергию, а также кинетическую энергию вращательного движения одной молекулы аммиака NH ₃ при температуре 27˚С.

64. Определить концентрацию n молекул кислорода, находящегося в сосуде вместимостью V = 2 л. Количество вещества v кислорода равно 0,2 моль.

65. В сосуде объемом 40 л находится кислород при темпеpатуpе 300 К. Когда часть газа израсходовали, давление в баллоне понизилось на 100 кПа. Определить массу израсходованного кислорода. (T = const)

66. В баллоне находился идеальный газ при давлении 40 МПа и температуре 300 К. Затем 3/5 газа выпустили, а температура понизилась до 240 К. Под каким давлением находится оставшийся в баллоне газ?

67. Определить среднее значение полной кинетической энергии одной молекулы гелия, кислорода и водяного пара при темпеpатуpе 400 К.

68. Трехатомный газ под давлением p = 200 кПа и температуре 20°С занимает объем, равный 10 л. Определить теплоемкость С_p этого газа при постоянном давлении.

69. В азоте взвешены мельчайшие пылинки, движущиеся так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна 6·10^{-10 г. Газ находится при темпеpатуpе 400 К. Определить средние квадратичные скорости и средние кинетические энергии поступательного движения молекулы азота и пылинки.}

70. При какой темпеpатуpе средняя кинетическая энергия поступательного движения молекулы газа равна 4,14·10^-21 Дж?

71. Какое давление создают 40 л водорода про темпеpатуpе 103˚С, если при нормальных условиях тот же газ занимает объем 364 л? Определить массу газа.

72. Баллон содержит 80 г кислорода и 320 г аргона. Давление смеси 1 МПа, температура 300 К. Принимая газы за идеальные, определить объем баллона.

73. Один баллон объемом 10 л содержит кислород под давлением 1,5 МПа, а другой баллон объемом 22 л содержит азот под давлением 0.6 МПа. Когда баллоны соединили между собой, оба газа смешались, образовав однородную смесь (без изменения темпеpатуpы). Найти парциальные давления обоих газов в смеси и полное давление смеси.

74. Газ при давлении 810 кПа и температуре 12˚С занимает объем 855 л. Каким будет давление, если тот же газ при температуре 320 К займет объем 800 л?

75. Какой объем занимает смесь азота массой 1 кг и гелия массой 1 кг при нормальных условиях?

76. В баллоне вместимостью 10 л находится гелий под давлением 1 МПа при температуре 300 К. После того, как из баллона было взято 1,0 г гелия, температура в баллоне понизилась до 200 К. Определить давление гелия, оставшегося в баллоне.

77. Определить количество вещества v и число молекул N кислорода массой m = 0,51 кг.

78. Чему равны суммарные кинетические энергии поступательного и вращательного движения всех молекул, находящихся в 2 кг водорода при темпеpатуpе 300 К?

79. Одноатомный газ при нормальных условиях занимает объем V = 6 л. Вычислить теплоемкость C_V этого газа при постоянном объеме.

80. Три баллона объемом V ₁ = 2 л, V ₂ = 3 л, V ₃ = 5 л заполнены кислородом под давлением p ₁ = 2 атм, p ₂ = 3 атм, p ₃ = 4 атм, соответственно. Определить давление, установившееся в баллонах после их соединения друг с другом. Процесс считать изотермическим.

81. Какое количество теплоты требуется для того, чтобы воздух массой 5 г от температуры 17˚С нагреть при постоянном давлении настолько, чтобы его объем увеличился в два раза?

82. В теплоизолированном цилиндре с поршнем находится 0,2 кг азота при темпеpатуpе 293 К. Азот, расширяясь, совершает работу 4470 Дж. Найти изменение внутренней энергии азота и его темпеpатуpу после расширения.

83. Азот массой 0,1 кг был изобарно нагрет от температуры T ₁ = 300 К до температуры T ₂ = 500 К. Определить работу A, совершенную газом, полученную им теплоту Q и изменение Δ U внутренней энергии азота.

84. Определить количество теплоты, поглощаемой водородом массой 0,2 кг при нагревании его от 0˚С до 100˚С при постоянном давлении. Найти также изменение внутренней энергии газа и совершаемую им работу.

85. Количество v = 2 кмоль углекислого газа нагревается при постоянном давлении на Δ Т = 50 К. Найти изменение внутренней энергии газа Δ U, работу A расширения газа, количество теплоты Q, сообщенное газу.

86. Кислород при неизменном давлении 80 кПа нагревается. Его объем увеличивается от 1 м³ до 3 м³. Определить изменение внутренней энергии, работу, а также теплоту, сообщенную газу.

87. Определить количество теплоты, которое надо сообщить кислороду объемом 50 л при его изохорном нагревании, чтобы давление газа повысилось на 0,5 МПа.

88. Какая работа А совершается при изотермическом расширении водорода массой m = 5 г, взятого при темпеpатуpе Т = 290 К, если объем газа увеличивается в три раза?

89. Азот, находящийся при нормальных условиях, расширяется адиабатически, увеличивая свой объем в 5 раз. Количество вещества азота 10 молей. Найти изменение внутренней энергии газа и совершенную им работу.

90. Определить работу, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты 21 кДж. Найти также изменение внутренней энергии газа.

91. При нагревании азота ему было передано 1000 Дж теплоты. Определить работу расширения при постоянном давлении.

92. Найти работу и изменение внутренней энергии при адиабатном расширении воздуха, если его объем увеличился в 10 раз. Начальная температура 15˚С, масса m = 0,29 кг.

93. Кислород массой 2 кг занимает объем 1 м³ и находится под давлением 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема 3м³, а затем при постоянном объеме до давления 0,5 МПа. Найти изменение внутренней энергии газа, совершенную им работу и количество теплоты, переданной газу. Построить график процесса в координатах V - p.

94. Определить, какое количество теплоты необходимо сообщить углекислому газу массой 220 г, чтобы нагреть его на 20 К: а) при постоянном объеме, б) при постоянном давлении?

95. Водород массой 40 г, имевший темпеpатуpу 300 К, адиабатно расширяется, увеличив объем в 3 раза. Затем при изотермическом сжатии объем газа уменьшился в два раза. Определить полную работу, совершенную газом и конечную температуру газа.

96. Азот массой 5 кг был изобарно нагрет на 150 К. Найти количество теплоты, сообщенное газу, изменение внутренней энергии, совершенную газом работу.

97. При изотермическом расширении азота при температуре 280 К его объем увеличился в два раза. Определить: 1) совершенную при расширении газа работу, 2) изменение его внутренней энергии, 3) количество теплоты, полученное газом. Масса азота 0,2 кг.

98. Во сколько раз увеличится объем водорода, содержащий количество вещества 0,4 моль, при изотермическом расширении, если при этом газ получил 2 кДж теплоты? Т = 300 К.

99. Объем водорода при изотермическом расширении (Т = 300 К) увеличился в 3 раза. Определить работу, совершенную газом, и полученное им количество теплоты. Масса водорода равна 200 г.

100. Определить работу А, которую совершит неон, если ему при постоянном давлении сообщить количество теплоты Q = 21 кДж. Найти также изменение ∆ U внутренней энергии газа.

101. Расстояние между зарядами Q ₁ = 100 нКл и Q ₂ = - 50 нКл равно d = 10см. Определить силу F, действующую на заряд Q ₃ = 1 мкКл, отстоящий на r ₁ = 12 см от заряда Q ₁ и на r ₂ = 10 см от заряда Q ₂.

102. Точечные заряды Q ₁ = 20 мкКл, Q ₂ = 10 мкКл находятся на расстоянии d = 5 см друг от друга. Определить напряженность поля в точке, удаленной на расстоянии r ₁= 4 см от первого и r ₂ = 3 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд Q = 2 мкКл.

103. Имеется два свободных положительных заряда 4 Q и Q, находящихся на расстоянии a друг от друга. Какой заряд и где нужно поместить, чтобы система находилась в равновесии.

104. Тонкое полукольцо радиусом R = 20 см несёт равномерно распределённый заряд Q =2 мкКл. Определить потенциал поля в центре кривизны полукольца.

105. На шелковой нити в воздухе подвешен шарик массой m = 100 мг. Шарику сообщен заряд Q ₁ = 2 нКл. На каком расстоянии от него следует поместить снизу заряд Q ₂ = -Q ₁, чтобы сила натяжения нити увеличилась в два раза.

106. Четыре одинаковых заряда Q = 15 нКл каждый закреплены в вершинах квадрата со стороной а = 15 см. Найти силу F, действующую на один из этих зарядов со стороны трёх остальных.

107. Имеются два закреплённых положительных заряда 4 q и q. Расстояние между зарядами ℓ. Как нужно расположить третий заряд q ₀, чтобы он находился в равновесии?

108. По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределен заряд Q = 20 нКл. Определить потенциал поля этого заряда в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.

109. Два положительных точечных заряда Q и 9 Q закреплены на расстоянии a = 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии.

110. Заряженная капелька жидкости массой m = 0,01 г находится в равновесии в поле горизонтально расположенного плоского конденсатора. Расстояние между пластинами конденсатора d = 4 мм, разность потенциалов между ними U = 200 В. Определить заряд капельки.

111. Тонкое кольцо радиусом R = 30 см несёт равномерно распределённый заряд Q = 3 мкКл. Определить потенциал поля в центре кольца.

112. Тонкое полукольцо радиусом R = 25 см несёт равномерно распределённый заряд Q = 4·10^-9 Кл. Определить потенциал поля в центре кривизны полукольца.

113. Электрическое поле создается двумя зарядами Q ₁ = 5 мкКл и Q ₂ = 3 мкКл, находящимися на расстоянии а = 0,1 м друг от друга. Определить работу А сил поля по перемещению заряда Q = 20нКл из точки один в точку два.

114. На расстоянии d = 20 см находятся два точечных заряда Q ₁ = - 50 нКл и Q ₂ = 100 нКл. Определить силу F, действующую на заряд Q ₃ = -10 нКл, удаленных от обоих зарядов на одинаковое расстояние, равное d = 20 см.

115. Тонкое полукольцо несёт равномерно распределённый с линейной плотностью t = 0,2 мкКл/м заряд. Найти потенциал поля в центре кольца.

116. Имеются два свободных положительных заряда 4 Q и Q, находящиеся на расстоянии а друг от друга. Какой заряд и где нужно поместить, чтобы вся система находилась в равновесии.

117. В вершинах при основании прямоугольного равнобедренного треугольника расположены одинаковые точечные заряды Q ₁ = Q ₂ = 2·10^-8 Кл. Расстояние между зарядами равно 0,6 м. Определить напряжённость электрического поля и потенциал в вершине прямого угла.

118. В вершинах правильного треугольника со стороной а = 10 см находятся заряды Q ₁ = 10 мкКл, Q ₂ = 20 мкКл и Q ₃ = 30 мкКл. Определить силу, действующую на заряд Q ₁ со стороны двух других зарядов.

119. Четыре одинаковых заряда Q = 10 нКл каждый, закреплены в вершинах квадрата со стороной а = 20 см. Найти силу F, действующую на один из этих зарядов со стороны трёх остальных.

120. По тонкому кольцу равномерно распределён заряд Q = 4 нКл с линейной плотностью t =50 нКл/м. Определить напряжённость Е электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удалённой от его центра на расстояние, равное половине радиуса.

121. Два элемента с ЭДС ℰ ₁ = ℰ ₂ = 4 В и внутренними сопротивлениями r ₁ = r ₂ = 0,5 Ом соединены с внешним сопротивлением R = 10 Ом как показано на рисунке. Определить силу тока на сопротивлении R и падение напряжения U на нём.

122. В схеме на рисунке ℰ ₁ = ℰ ₂ = 4 В, r ₁ = r₂ = 0,5 Ом, R = 10 Ом. Определить силу тока и напряжение на сопротивлении R.

123. Определить силу тока I ₃, показываемую амперметром в схеме. Напряжение на зажимах элемента в замкнутой цепи равно 2,1 В; R ₁ = 5 Ом; R ₂ = 6 Ом; R ₃ = 3 Ом. Сопротивлением амперметра пренебречь.

124. Две батареи (ℰ ₁ = 6 В и ℰ ₂ = 8 В) и три сопротивления R ₁ = 4 Ом, R ₂ = 8 Ом и R ₃ = 8 Ом соединены, как показано на рисунке. Определить силу тока I ₃.

125. Определить КПД схемы, если R ₁ = 2 Ом; R ₂ = 5 Ом; r = 0,5 Ом.

126. В схеме на рисунке ℰ ₁ = 2,1 В; ℰ ₂ = 1,9 В; R ₁ = 45 Ом; R ₂ =10 Ом; R ₃ = 10 Ом. Определить токи I ₁, I ₂, I ₃.

127. В схеме на рисунке ℰ ₁ = 12 В, r ₁ = 2 Ом, ℰ ₂ = 24 В, r ₂ = 6 Ом, сопротивление R = 16 Ом. Определить токи I ₁, I ₂, I.

128. Две батареи (ℰ ₁ = 6 В и ℰ ₂ = 5 В) с внутренними сопротивлениями r ₁ = 1 Ом и r ₂ = 2 Ом и внешнее сопротивление R = 10 Ом соединены как показано на рисунке. Определить токи I ₁, I ₂ и I.

129. В схеме на рисунке ℰ ₁ = 2 В, ℰ ₂ = 1 В, R ₁ = 10 Ом, R ₂ = 500 Ом, R ₃ = 300 Ом. Определить силу тока I ₁ на сопротивлении R ₁.

130. В схеме на рисунке ℰ ₁ = 6 В, ℰ ₂ = 8 В, сопротивления R ₁ = 4 Ом, R ₂ = 8 Ом, R ₃ = 6 Ом. Определить силу тока I ₃ на сопротивлении R ₃.

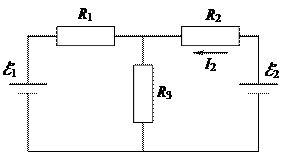
131.	R = 6 Ом
ℰ 1 = 2,2 В
ℰ 2 = 2,4 В
r 1 = 0,8 Ом
r 2 = 0,2 Ом
I -? U -?

132. В схеме на рисунке ℰ ₁ = 1,5 В, ℰ ₂ = 2 В, R ₁ = 50 Ом, R ₂ = 15 Ом, R ₃ = 15 Ом. Определить токи I ₁, I ₂, I ₃.

133.	ℰ 1 = 12 В
r 1 = 2 Ом
ℰ 2 = 24 В
r 2 = 6 Ом
R = 16 Ом
I 1 -? I 2 -?
I -?

134.	ℰ 1 = 8 В
ℰ 2 = 6 В
R 1 = 4 Ом
R 2 = 6 Ом
R 3 = 8 Ом
UAB -?

135.	R 1 = 100 Ом
R 2 = 50 Ом
R 3 = 20 Ом
ℰ 1 = 2 В
I 3 = 50 мА
ℰ 2 -?

136.	R = 6 Ом
	ℰ 1 = 2,2 В
	ℰ 2 = 2,4 В
	r 1 = 0,8 Ом
	r 2 = 0,2 Ом
	I -? U -?

137.	ℰ 1 = 12 В
r 1 = 1 Ом
ℰ 2 = 6 В
r 2 = 1,5 Ом
R = 20 Ом
I 1 -? I 2 -?
I -?

138.	ℰ 1 = 10 В
r 1 = 2 Ом
ℰ 2 = 24 В
r 2 = 6 Ом
R = 20 Ом
I 1 -? I 2 -?
I -?

139.	ℰ 1 = 2 В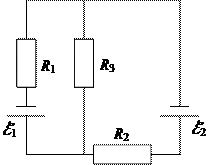
ℰ 2 = 1 В
R 1 = 1000 Oм
R 2 = 500 Ом
R 3 = 200 Ом
I 1 -?

140.	ℰ 1 = 6 В
ℰ 2 = 8 В
R 1 = 4 Ом
R 2 = 8 Ом
R 3 = 6 Ом
I 2 -?

141. По двум параллельным бесконечно длинным проводникам в одном направлении текут токи 10 А и 30 А соответственно. Найти напряженность магнитного поля в точке, расположенной посередине между проводниками, если расстояние между проводниками равно 10 см.

142. По тонкому проводящему кольцу радиусом R = 10 см течёт ток I = 80 А. Найти магнитную индукцию В в точке А, равноудалённой от всех точек кольца на расстоянии r = 20 см.

143. Бесконечно длинный провод образует круговую петлю, касательную к проводу. По проводу идет ток силой 5 А. Найти радиус петли, если известно, что напряженность магнитного поля в центре петли равна 50 А/м.

144. Найти напряженность поля в центре квадратной рамки, по которой течет ток 20 А. Сторона рамки равна 20 см.

145. Два длинных прямых параллельных проводника, по которым текут в противоположных направлениях токи I ₁ = 0,2 А и I ₂ = 0,4 А находятся на расстоянии ℓ = 14см. Найти индукцию магнитного поля в точке расположенной между проводниками на расстоянии r = 4 см от первого из них.

146. Ток в 20 А течет по длинному проводнику, согнутому под прямым углом. Найти напряженность магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии 15 см.

147. Ток в I = 15 А, протекая по проволочному кольцу из медной проволоки сечением S = 1,0 мм², создает в центре кольца напряженность магнитного поля Н = 10 А/м. Какая разность потенциалов приложена к концам проволоки, образующей кольцо?

148. По двум длинным прямым параллельным проводникам в одном направлении текут токи I ₁= 1 А и I ₂ = 3 А. Расстояние между проводниками r = 40 см. Найти индукцию магнитного поля в точке, находящейся посередине между проводами.

149. Два длинных параллельных проводника, по которым текут в противоположных направлениях токи I ₁ = 0,2 А и I ₂ = 0,4 А, расположены на расстоянии r = 12 см друг от друга. Определить индукцию магнитного поля в точке, лежащей в середине отрезка прямой, соединяющей проводники.

150. Найти напряженность и индукцию магнитного поля в общем центре О двух круговых контуров с радиусами r ₁ = 60 см и r ₂ = 40 см, по которым в противоположных направлениях идут токи I ₁ = 20 А и I ₂ = 40 А. Контуры лежат в одной плоскости. Среда - воздух.

151. По бесконечно длинному проводу изогнутому так, как это показано на рисунке, течёт ток I = 200 A. Определить магнитную индукцию В в точке О. Радиус дуги R = 10 см.

152. Ток в 18 А идёт по длинному проводу, согнутому под прямым углом. Найти напряжённость магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии 15 см.

153. Ток 20 А идёт по длинному проводу, согнутому под прямым углом. Найти напряжённость магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершин угла на расстояние 10 см.

154. По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2 I (I = 100 А). Определить магнитную индукцию В в точке А. Расстояние d = 10 см.

155. Ток в 20 А, протекая по проволочному кольцу из медной проволоки сечением S = 1 мм², создают в центре кольца напряжённость магнитного поля Н = 10 А/м. Какая разность потенциалов приложена к концам проволоки, образующей кольцо?

156. Из проволоки длиной ℓ = 3,14 м и сопротивлением R = 2 Ом сделали кольцо. Определить индукцию магнитного поля в центре кольца, если на концах провода создана разность потенциалов U = 1 В.

157. Два круговых витка расположены в двух взаимно-перпендикулярных плоскостях так, что центры этих витков совпадают. Радиус каждого витка 2 см и токи, текущие по виткам I ₁ = I ₂ = 5 А. Найти напряжённость магнитного поля в центре этих витков.

158. По кольцевому проводнику радиусом R = 10 см течёт ток силой 4 А. Параллельно плоскости кольцевого проводника на расстоянии 2 см над его центром проходит бесконечно длинный прямолинейный проводник, по которому течёт ток силой 2 А. Определить индукцию и напряжённость магнитного поля в центре кольца. Решение пояснить рисунком.

159. Катушка длиной 30 см состоит из 10 витков. Найти напряжённость магнитного поля внутри катушки, если ток, проходящий по катушке, равен 2 А. Диаметр катушки считать малым по сравнению с её длиной.

160. Два бесконечно длинных, пересекающихся под прямым углом проводника с токами I ₁ = 20 А и I ₂ = 30 А лежат в плоскости чертежа. Найти напряженность и индукцию магнитного поля в точке М, лежащей на расстоянии а = 40 см от первого и b = 20 см от второго проводника.

Список рекомендуемой литературы

1. Трофимова, Т.И. Курс физики: учеб. пособие для вузов. - 11-е изд., стер. / Т.И. Трофимова. – М.: Изд. центр «Академия», 2006. – 558 с.

2. Детлаф, А.А. Курс физики: учеб. пособие для студ. втузов. - 6-е изд., стер. / А.А. Детлаф, Б.М. Яворский. - М.: Изд. центр «Академия», 2007. – 719 с.

3. Яворский, Б.М. Справочник по физике / Б. М. Яворский, А. А. Детлаф. – 3-е изд., испр. – М.: Наука, 1990. – 624 с.

4. Физика. Механика. Методические указания по выполнению расчётно-графической работы для студентов инженерно-технических специальностей. / Брянск. гос. технол. акад. Сост. Е.А. Вощукова. – Брянск: БГИТА, 2001. – 15 с.

5. Физика. Молекулярная физика и термодинамика. Сборник методических указаний по выполнению расчётно-графической работы (молекулярная физика и термодинамика) для студентов инженерно-технических специальностей. / Брянск. гос. технол. акад. Сост. Ю.А. Ивашкин, М.Д. Преженцев. – Брянск: БГИТА, 2001. – 20 с.

6. Механика. Сборник методических указаний для самостоятельной работы студентов БГИТА дневного и заочного обучения. / Брянск. гос. технол. акад. Сост. М.Д. Преженцев, О.В. Рогазинская. – Брянск: БГИТА, 2005. – 66 с.

7. Молекулярная физика и термодинамика. Сборник методических указаний для самостоятельной работы студентов БГИТА дневного и заочного обучения. / Брянск. гос. технол. акад. Сост. В.А. Матанцева, Л.М. Притыченко. – Брянск: БГИТА, 2005. – 33 с.

8. Волькенштейн, В.С. Сборник задач по общему курсу физики: для втузов / В. С. Волькенштейн. – 3-е изд., испр. и доп. – СПб.: Кн. мир, 2007. – 327 с.

9. Трофимова, Т.И. Сборник задач по курсу физики с решениями: учеб. пособие для вузов / Т. И. Трофимова, З. Г. Павлова. – 7-е изд., стер. – М.: Высш. шк., 2006. – 591 с.

Царьковская Надежда Ивановна

Плескачева Ольга Юрьевна

ФИЗИКА

Задания к расчетно-графической работе №1

по физике для студентов бакалавриата по направлениям

250100 «Лесное дело» и 250700 «Ландшафтная архитектура» очной формы обучения

Лицензия НД № 14185 от 6.03.2001 г

Формат 60×94 1/16. Тираж 50 экз. Печ. л. – 1,5

Брянская государственная инженерно-технологическая академия.

241037. г. Брянск, пр. Станке Димитрова, 3, редакционно-издательский

отдел. Подразделение оперативной печати

Подписано к печати

Дата добавления: 2015-07-20