Расчет участка оболочки над уровнем жидкости

Рассмотрим участок ВС (см. рис. 1). На расстоянии у от полюса А отсечем часть оболочки нормальным коническим сечением с углом широты φ (рис. 2).

Определим границы 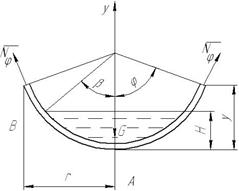участка ВС 90 ≥ φ≥ β. Рассмотрим равновесие отсеченной части оболочки.

Составим уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось у для отсеченной части оболочки.

Оно имеет вид: 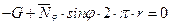, где G -вес жидкости, заполняющей полусферу; φ, r –координаты расчетного сечения; 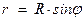– текущий радиус кольцевого сечения оболочки на расстоянии y от полюса; 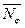– меридиональная погонная сила.

Вес жидкости определяется по формуле

,

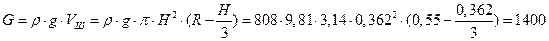где V_ш – объем шарового сегмента, заполненного жидкостью:

,

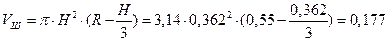H -высота столба жидкости в полусферической оболочке: 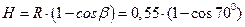. Находим погонное меридиональное усилие 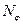из уравнения равновесия отсеченной части оболочки:

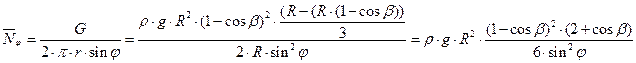Определим погонное кольцевое усилие N_θ для участка ВС, используя уравнение Лапласа:

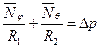
где R₁,R₂ – главные радиусы кривизны расчетного сечения оболочки;

∆p – интенсивность внешней нагрузки на стенку в расчетном сечении оболочки.

Так как для сферы R₁ = R₂, а для участка ВС ∆р = 0, то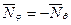

Результаты расчета заносим в таблицу 1. при условии 90 ≥ φ ≥ β.

Таблица 1

N точки	φ, град	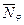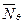, Н/м	, Н/м
		405,2	-405,2
		407,2	-407,2
		413,2	-413,2
		423,5	-423,5
		438,5	-438,5
		458,8	-458,8

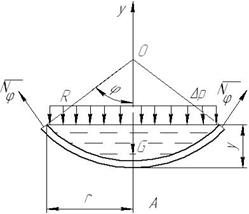2. Расчет участка оболочки под уровнем жидкости

Рассмотрим участок оболочки АВ (см. рис. 1). Построим нормальное коническое сечение на расстоянии у от полюса оболочки. Положение расчетного сечения определяем координатами r, φ (рис. 3).

Определим границы участка АВ: β≥φ≥0.

Рис. 3. Расчетная схема для участка оболочки под уровнем жидкости  

Составим уравнение равновесия для отсеченной части оболочки в проекции на вертикальную ось у.

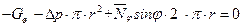
где G_ш – вес жидкости, заключенной в шаровом сегменте высотой y;

∆p – давление жидкости в расчетном сечении;

π ⋅ r² – площадь поперечного сечения оболочки на уровне y;

r = R ⋅ sinφ – радиус поперечного сечения оболочки на уровне y.

Определим составляющие уравнения равновесия.

Вес жидкости

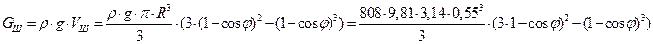где V_ш – объем шарового сегмента: , .

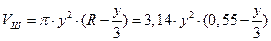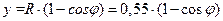Давление жидкости на уровне (H − y) от зеркала жидкости

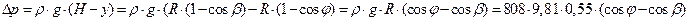Площадь поперечного сечения .

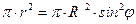Подставим найденные значения G, ∆p, r в уравнение равновесия и определим меридиональное усилие :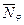

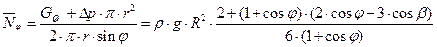
Получим выражение для погонного кольцевого усилия 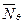, используя уравнение Лапласа. При R₁ = R₂ = R уравнение Лапласа имеет вид

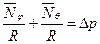, отсюда получаем

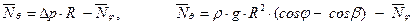
Результаты расчета заносим в таблицу 2.2 при условии β ≥ φ ≥ 0.

Таблица 2

N точки	φ, град	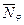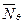, Н/м	, Н/м
		458,8	-458,8
		549,5	-28,7
		642,4	319,4
		720,1	576,8
		771,1	735,3
		788,8	788,8

По данным таблиц 1 и 2 строим эпюры погонных усилий. Пример эпюры приводится на рис.4.

С помощью эпюры определяем наиболее напряженное сечение оболочки и максимальные погонные усилия .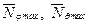

Дата добавления: 2015-07-20