Приклад виконання.

1. Засоби представлення графу.

Матриця суміжностей:

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

Матриця інцидентностей.

DM

DU

DP

MU

MS

MR

MH

UP

US

ST

PH

PR

TR

TH

D

M

U

H

P

S

T

R

Список суміжності.

D	M	P	U
M	D	U	S	R	H
U	D	M	P	S
H	M	P	T
P	D	U	H	R
S	U	M	T
T	S	H	R
R	M	P	T

2. Визначення всіх метричних характеристик графу.

Кількість верхівок: 8.

Кількість ребер: 14.

Ступені верхівок:

D	M	U	H	P	S	T	R

Дистанції між парами верхівок.

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

Радіуси верхівок.

D	M	U	H	P	S	T	R

Діаметр графу: 3.

Радіус графу: 2.

Хроматичне число графу.

Хроматичне число графу дорівнює 3.

Хроматичний клас графу.

Хроматичний клас графу дорівнює 5.

3. Алгоритм Флойду для графу.

Первинна матриця відстаней матриця шляху

	D	M	U	H	P	S	T	R
D				∞		∞	∞	∞
M					∞		∞
U				∞			∞	∞
H	∞		∞			∞		∞
P		∞				∞	∞
S	∞			∞	∞			∞
T	∞	∞	∞		∞
R	∞		∞	∞		∞

	D	M	U	H	P	S	T	R
D		M	U		P
M	D		U	H		S		R
U	D	M			P	S
H		M			P		T
P	D		U	H				R
S		M	U				T
T				H		S		R
R		M			P		T

Робота алгоритму.

Через верхівку D:

	D	M	U	H	P	S	T	R
D				∞		∞	∞	∞
M							∞
U				∞			∞	∞
H	∞		∞			∞		∞
P						∞	∞
S	∞			∞	∞			∞
T	∞	∞	∞		∞
R	∞		∞	∞		∞

	D	M	U	H	P	S	T	R
D		M	U		P
M	D		U	H	D	S		R
U	D	M			P	S
H		M			P		T
P	D	D	U	H				R
S		M	U				T
T				H		S		R
R		M			P		T

Через верхівку М:

	D	M	U	H	P	S	T	R
D							∞
M							∞
U							∞
H
P							∞
S
T	∞	∞	∞		∞
R

	D	M	U	H	P	S	T	R
D		M	U	M	P	M		M
M	D		U	H	D	S		R
U	D	M		M	P	S		M
H	M	M	M		P	M	T	M
P	D	D	U	H		M		R
S	M	M	U	M	M		T	M
T				H		S		R
R	M	M	M	M	P	M	T

Через верхівку U:

	D	M	U	H	P	S	T	R
D							∞
M							∞
U							∞
H
P							∞
S
T	∞	∞	∞		∞
R

	D	M	U	H	P	S	T	R
D		M	U	M	P	M		M
M	D		U	H	U	S		R
U	D	M		M	P	S		M
H	M	M	M		P	M	T	M
P	D	U	U	H		U		R
S	M	M	U	M	U		T	M
T				H		S		R
R	M	M	M	M	P	M	T

Через верхівку H:

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

	D	M	U	H	P	S	T	R
D		M	U	M	P	M	M	M
M	D		U	H	U	S	H	R
U	D	M		M	P	S	M	M
H	M	M	M		P	M	T	M
P	D	U	U	H		U	H	R
S	M	M	U	M	U		T	M
T	H	H	H	H	H	S		R
R	M	M	M	M	P	M	T

Через верхівку P:

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

	D	M	U	H	P	S	T	R
D		M	U	P	P	M	P	P
M	D		U	H	U	S	H	R
U	D	M		P	P	S	P	P
H	P	M	P		P	M	T	P
P	D	U	U	H		U	H	R
S	M	M	U	M	U	M	T	M
T	H	H	H	H	H	S		R
R	P	M	P	P	P	M	T

Через верхівку S:

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

	D	M	U	H	P	S	T	R
D		M	U	P	P	M	M	P
M	D		U	H	U	S	S	R
U	D	M		P	P	S	S	P
H	P	M	P		P	M	T	P
P	D	U	U	H		U	H	R
S	M	M	U	M	U	M	T	M
T	S	S	S	H	H	S		R
R	P	M	P	P	P	M	T

Через верхівку T: - змін немає

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

	D	M	U	H	P	S	T	R
D		M	U	P	P	M	M	P
M	D		U	H	U	S	S	R
U	D	M		P	P	S	S	P
H	P	M	P		P	M	T	P
P	D	U	U	H		U	H	R
S	M	M	U	M	U	M	T	M
T	S	S	S	H	H	S		R
R	P	M	P	P	P	M	T

Через верхівку R Вихіднi таблицi.

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

	D	M	U	H	P	S	T	R
D		M	U	P	P	M	P	P
M	D		U	H	R	S	S	R
U	D	M		P	P	S	P	P
H	P	M	P		P	M	T	P
P	D	R	U	H		R	R	R
S	M	M	U	M	M	M	T	M
T	R	S	R	H	R	S		R
R	P	M	P	P	P	M	T

Матриця досяжності

Орієнтований граф:

	D	M	U	H	P	S	T	R
D
M
U
H
P
S
T
R

4. Пошук максимального потоку в мережі (метод Форда-Фалкерсона).

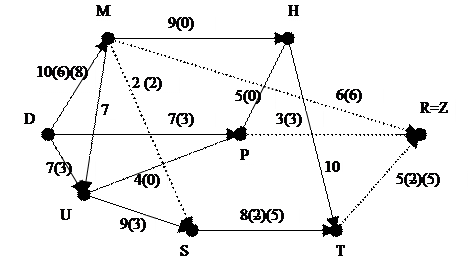
Етап насичення:

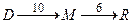min=6

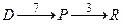min=3

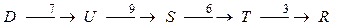
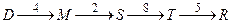min=2

min=3;

Усі ребра, що входять до стоку заповнені. Тобто максимальний проток цієї мережі Ф=6+3+5=8+3+3=14.

5. Ейлерів ціпок та цикл.

В цьому графі наявні 6 верхівок з непарними ступенями, тому побудова ейлеревого ціпку та циклу неможлива.

6. Задача комівояжера. Гамільтоновий ціпок та цикл.

Показано початок побудови дерева рішення.

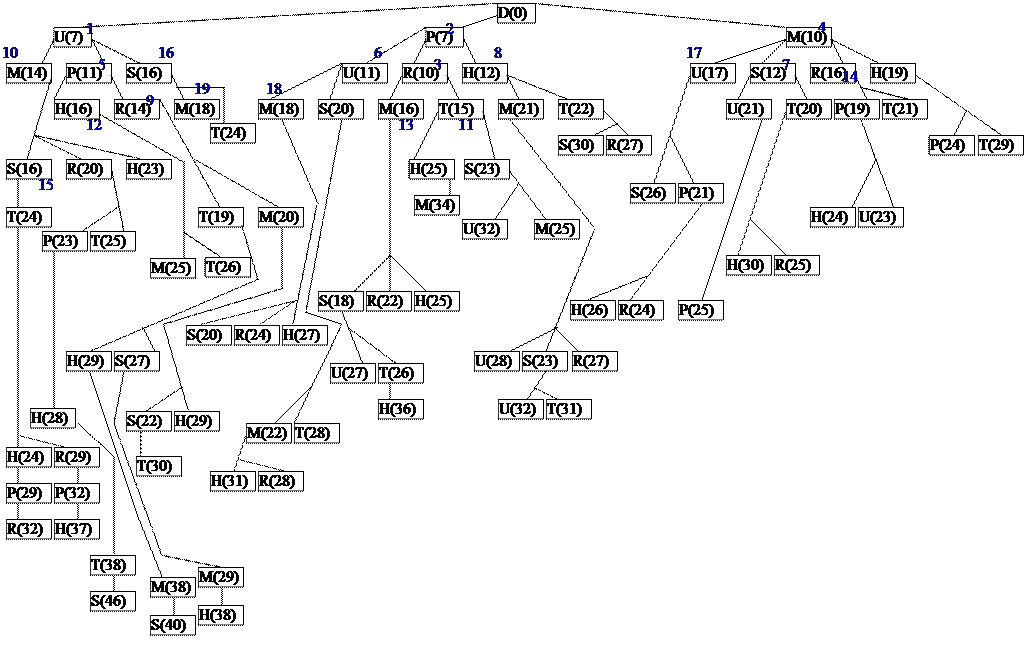Дата добавления: 2015-07-20