ЦП уравновешивающего (компенсационного) преобразования

Классификацию ЦП уравновешивающего преобразования наи­более естественно выполнить по используемому методу уравновеши­вания, являющемуся в этом случае наиболее важным признаком. Однако предварительный анализ существующих принципов построения таких ЦП показывает, что необходимо предварительно разбить их на два отличающихся друг от друга класса – ЦП последовательного во времени уравновешивания и ЦП параллельно-последовательного во времени уравновешивания.

Рассмотрим вначале некоторые общие вопросы методики измерений. Как известно, существуют два классических метода измерения – нулевой метод и метод совпадений. В первом случае берется одна мера, равная единице измерения, и используется столько раз (рисунок 3, а), сколько единиц в измеряемой величине. Если в измеряемой величине N единиц, топри этом потребуется N операций сравнения (при измерении длины мера N раз прикладывается к измеряемому предмету).

Во втором случае составляется «линейка» из соот­ветствующего количества N_maх, единичных мер, чтобы перекрыть весь диапазон возможного изменения измеряемой величины. Измеряемая величина (рисунок 3, б) сравнивается (при измерении длины измеряе­мый предмет прикладывается к линейке) с подобной «линейкой» за одну операцию. Этот метод измерения электрических напряжений применяют, например, в амплитудных анализаторах (см. рисунок 2, б). В чистом виде в ЦП оба метода используют сравнительно редко, так как простейший вариант нулевого метода требует максимального количества операций сравнения, т. е. максимального времени измерения, а метод совпадений требует максимального количества мер, т.е. наиболее сложен по оборудованию. Однако можно говорить о существовании двух принципиально различных вариантах выполнения операций сравнения — последовательно и параллельно во времени. С целью устранения указанных недостатков оба метода можно усовершенствовать.

Если в нулевом методе увеличить количество мер до М, то количество операций сравнения Н может быть существенно сокращено Например, выбирая значения мер по двоичной системе (2°; 2¹.., 2^м-1), можно показать, что

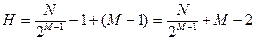. (1)

Рисунок 3 – Сравнение последовательного и параллельно-последовательного во времени уравновешивания

Пусть N = 256. Тогда при М = 1 необходимо 255 операций срав­нения, а при М = 4 — только 34.

Количество мер и их значения можно выбирать по-разному, в зави­симости от принципа действия, принятой системы счисления и числа разрядов отсчета ЦП. Алгоритмы процесса уравновешивания, т. е. последовательность использования мер и разрядов, также могут быть весьма разнообразными. Однако главный признак — последователь­ность во времени отдельных операций сравнения — сохраняется и используется в большинстве ЦИП уравновешивающего преобразова­ния.

В классическом варианте метода совпадений уравновешивание отсутствует. Если увеличить количество операций сравнения до Н, то количество необходимых мер М может быть существенно сокра­щено. При этом появляются разряды, в каждом из которых операции сравнения проводятся параллельно во времени, а оценка каждого из разрядов осуществляется последовательно во времени. В каждом из разрядов (кроме последнего) необходимо осуществлять уравнове­шивание, т. е. на следующий разряд должна подаваться разность между входной и компенсирующей величинами предыдущего разряда.

Выбирая величины мер, например, по десятичной системе (1, 2,..., 9), можно показать, что при заданном числе H операций сравнения (а по существу числе разрядов отсчета) необходимое число мер

. (2)

Пусть N_max =999. Тогда при Н = 1 необходимо 999 мер, а при Н = 3 — только 27.

Рисунок 3, в иллюстрирует особенности последовательного, а рисунок 3, г — параллельно-последовательного во времени уравнове­шивания. При параллельно-последовательном во времени уравнове­шивании количество разрядов и мер в разрядах определяется принятой системой счисления и может быть различным, так же как и сам алго­ритм процесса уравновешивания. Однако главный признак, в отличие от последовательного уравновешивания, - наличие параллельных во времени операций сравнения, хотя бы минимум двух. Принцип параллельно-последовательного во времени уравновешивания, несмотря на на ряд преимуществ, стал использоваться в ЦП сравнительно недавно, и его возможности еще недостаточно изучены. В технической литературе его иногда называют прямым уравновешиванием.

Далее ЦП уравновешивающего преобразования целесообрапзно классифицировать по известным способам уравновешивания, существенно отличающимся друг от друга, т.е. подразделить оба класса на ЦИП развертывающего и следящего уравновешивания. И в том, и в другом способе можно использовать произвольные системы счисления, количество мер, количество разрядов и алгоритмы осуществле­ния процесса уравновешивания в зависимости от достигаемых кон­кретных характеристик данного ЦП. Однако между этими способами имеется и различие, наиболее существенное с точки зрения величины динамической погрешности и надежности ЦП.

Основной особенностью способа развертывающего уравн о в е- ш и в а н и я (рисунок 4) является осуществление необходимых операций сравнения измеряемой х и компенсирующей у величин по определенной наперед заданной программе, в процессе выполнения которой величина у меняется в пределах от 0 до y_max = x_max. Отсчет осуществляется в момент равенства с заданной точностью величин х и у. Чтобы производить постоянное измерение, такой процесс надо повторять периодически.

Рисунок 4 - Схема ЦИП Рисунок 5 – Схема ЦИП

развертывающего уравновешивания следящего уравновешивания

На рисунке 4,а показана укрупненная структурная схема ЦП развертывающего уравновешивания. Программирующее устройство ПУ изменяет компенсирующую величину y через промежуточный преобразователь П по определенной программе, например, равномерными ступенями, как показано на рисунке 4,б.

Одновременно изменяется и состояние цифрового отсчетного устройства ЦОУ. Величины x и y сравниваются сравнивающим устройством СУ и в момент их равенства через устройство управления УУ посылается сигнал, фикси­рующий состояние ЦОУ. Момент отсчета может быть вначале или в конце цикла изменения у.

При следящем уравновешивании (рисунок 5) изме­ряемая величина х непрерывно сравнивается с компенсирующей у, и при наличии разности x – y устройство управления через преобразователь обратной связи ПОС изменяет y в функции времени до тех пор, пока созданной точностью не будет достигнуто их установившееся равенство, после чего происходит цифровой отсчет.

Рисунок 6 – Динамическая погрешность при развертывающем (а) и следящем (б) уравновешивании

Если измеряемая величина х постоянна во времени, то преимуществом следящего уравновешивания по сравнению с развертывающим является в общем случае только возможность обеспечения большей надежности прибора, так как после выполнения первого измерения состояние всех узлов прибора не будет изменяться до тех пор, пока не изменится значение х. При развертывающем уравновешивании состояние всех узлов периодически изменяется независимо от характера изменения х (см. рисунок 5).

Если же измеряемая величина х изменяется во времени, то другим существенным преимуществом следящего уравновешивания является при прочих равных условиях меньшая динамическая погрешность ЦИП.

Предположим, что в обоих случаях ЦИП работает в режиме периодических измерений (циклов). При развертывающем уравновешивании (рисунок 6 ,а) к концу цикла отсчитанное значение х не будет соответствовать его действительному значению, т.е. появится динамическая погрешность. При следящем уравновешивании (рисунок 6, б) до определенной максимальной скорости изменения х такой погрешности не будет, что является существенным преимуществом ЦИП следящего уравновешивания.

В ряде случаев следящее уравновешивание в чистом виде создает неудобства при цифровой регистрации непрерывных процессов, так как не дает координаты времени. Однако это легко устранить введением дополнительного генератора циклов отсчета (аналогично развертывающему уравновешиванию), как показано на рисунке 6, б. Цифровая печать при этом производится после каждого цикла, т. е. Координата времени легко устанавливается по регистрирующему документу, и совершенно не обязателен после каждого цикла отсчета сброс компенсирующей величины, характерный для развертывающего уравновешивания.

ЦИП уравновешивающего преобразования применяют в основном для измерения электрических величин (напряжений, сопротивлений и т. п.), так как большинство других величин легко преобразуются в электрические.

ЦИП как развертывающего, так и следящего уравновешивающего преобразования, несмотря на разнообразие схем, можно характеризовать количеством параметров, по которым осуществляется процесс уравновешивания. С этой точки зрения целесообразно выделить в качестве самостоятельной группу ЦИП с уравновешиванием по двум параметрам, обладающую рядом особенностей.

ЦИП с уравновешиванием по двум параметрам предназначены для измерения переменных напряжений, комплексных сопротивлений и других аналогичных параметров. Они характеризуются необходи­мостью выполнения двух самостоятельных процессов уравновешива­ния, независимых друг от друга или взаимосвязанных, что обуслов­ливает особенности их построения. Такие ЦИП в зависимости от назначения можно выполнять как на контактных, так и на бескон­тактных переключающих элементах.

Для получения определенных характеристик в ЦИП можно осу­ществлять различные комбинации методов, приведенных в данной классификации. Так, например, в одной части структурной схемы ЦИП можно использовать уравновешивающее преобразование, а в другой — прямое преобразование и т. п. Подобные ЦИП не имеет смысла выде­лять в самостоятельную группу, так как составляемые комбинации могут быть самыми разнообразными.

ЦИП, не относящиеся к классу прямого преобразования, часто называют «ЦИП поразрядного кодирования», что, однако, не отра­жает основного признака таких ЦИП — наличия процесса уравнове­шивания с помощью общей отрицательной обратной связи. Кроме того, термин «поразрядное» не может быть общим классификационным признаком, так как определяет только алгоритм отработки уравнове­шивающей величиной значения измеряемой величины, который может быть различным в зависимости от построения схемы устройства управ­ления ЦИП. В общем же случае «поразрядное кодирование» суще­ствует в любом ЦИП и не может служить отличительным признаком.

Помимо термина №поразрядное кодирование» часто употребляют его синонимы «поразрядное уравновешивание» и «кодо-импульсное преобразование». Последнее название также неудачно, тем более, что ГОСТ определяет «кодо-импульсный метод преобразования» как метод, основанный на преобразовании значений непрерывной измеряемой величины в цифровой код и осуществляемый путем последовательного сравнения значения измеряемой величины с рядом дискретных значений известной величины, изменяющимся по определенному закону. Следовательно, это определение относится только к ЦИП последова­тельного во времени развертывающего уравновешивания и не охватывает ни следящего уравновешивания, ни параллельно-последовательного во времени уравновешивания.

2 Практическая часть

А) Представить группы чисел согласно вариантам таблицы 1:

а) в десятичной системе счисления;

б) в двоичной системе счисления;

в) в тетрадно-десятичной системе счисления:

Таблица 1.

NN п/п вариантов

Числа

Группы чисел

1 группа чисел

2 группа чисел

Продолжение таблицы 1.

NN п/п вариантов

Числа

Группы чисел

3 группа чисел

4 группа чисел

Продолжение таблицы 1.

NN п/п вариантов

Числа

Группы чисел

5 группа чисел

6 группа чисел

Б) Данные перевода чисел в коды указанных систем счисления свести в общую таблицу.

3 Отчетность по лабораторной работе

Для защиты лабораторной работы занятий студент должен представить отчет, выполненный согласно ГОСТ. Объем отчета должен быть не более 10 листов формата А4, графически он может быть выполнен от руки или на принтере.

В отчете должны быть представлены:

- титульный лист;

- введение;

- практическая часть;

- заключение;

- список литературы.

Контрольные вопросы

1 На какие классы делятся цифровые приборы?

2 Какие существуют варианты структурных схем АЦП?

3 Какова структура цифровых приборов прямого преобразования?

4 Какова структура цифровых приборов уравновешивающего (компенсационного) преобразования?

5 Что такое ЦП пространственного преобразования?

6 Что такое ЦП число-импульсного преобразования?

7 Что такое ЦП частотного преобразования?

8 Что такое ЦП временного преобразования?

9 Что такое ЦП амплитудного преобразования?

10 Что такое ЦП последовательного во времени уравновешивания?

11 Что такое ЦП параллельно-последовательного времени уравновешивания?

Литература

1 Евланов Л.Г. Контроль динамических систем. – М.: Наука, 1979.

2 ГОСТ 18242 – 72. качество продукции. Статистический премочный контроль по альтернативному признаку. Одноступенчатые и двухступенчатые корректируемые планы контроля.

3 ГОСТ 8. 508 – 84. Метрологические характеристики средств измерений и точностные характеристики средств автоматизации ГСП. Общие методы оценки и контроля.

4 Шляндин В.М. Цифровые измерительные преобразователи и приборы, Учебник для специальности «Информационно-измерительная техника». М.: «Высшая школа», 280 с. с ил.,1973.

Дата добавления: 2015-07-20