|
Читайте также: |
При исследовании торгового баланса необходимо провести динамику его основных показателей, чтобы выявить сложившуюся внешнеэкономическую тенденцию, без исследования которой суть данной работы не будет окончательной. Целесообразно использовать статистический метод исследования динамики на основе ряда цепных и базисных показателей. Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными. При построении динамических рядов необходимо соблюдать сопоставимость уровней динамического ряда. Для наглядного представления изменения экспорта и импорта в течение 5 лет по внешнеторговой деятельности РФ составим таблицу 3.8. (Приложение 8)
Таблица 3.8.
Расчет цепных и базисных показателей динамики
| Год | 
Импорт/Экспорт, млдр. дол.
| Абсолютный прирост, млрд. долл. | Темп роста, % | Темп прироста, % | ||||
| базисный | цепной | базисный 
| цепной | базисный
| цепной | |||
| 115,1 | - | - | - | - | - | - | ||
| 149,9 | 34,8 | 34,8 | 130% | 130% | 30% | 30% | ||
| 155,6 | 40,5 | 5,7 | 135% | 104% | 35% | 4% | ||
| 168,3 | 53,2 | 12,7 | 146% | 108% | 46% | 8% | ||
| 212,0 | 96,9 | 43,7 | 184% | 126% | 84% | 26% | ||
| Итого: | 800,9 | 225,4 | 96,9 | - | - | - | - |
Для более глубокого понимания характера явления проанализируем показатели динамики комплексно, то есть рассчитаем средние показатели. Средний уровень ряда характеризует обобщенную величину абсолютных уровней:
= 
= 
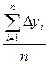Средний абсолютный прирост (убыль) - обобщающий показатель скорости изменения уровней во времени:
а) простая средняя из цепных изменений:
∆ = 
= 
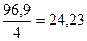
б) по первичному динамическому ряду:
∆ = 
= 
в) Средний коэффициент роста и темп роста - сводные обобщающие характеристики интенсивности изменения уровней ряда:
= 
= 
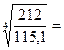1,0732
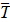
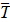= * 100% = 1,0732*100% = 107,32%
г) Средний темп прироста (сокращения):
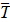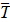∆ = - 100% = 107,32% - 100% = 7,32%
Исходя из рассчитанных показателей, можно сказать, что в среднем за 5 лет объем экспорта и импорта составлял 160,18 млрд. долл., при этом он в среднем ежегодно увеличивался в 1,0732 раза или 7,32% (24,23 млрд. долл.).
Так как средние величины дают обобщающую характеристику совокупности и не раскрывают ее структуры, то поэтому дополнительно рассчитывают показатели дисперсии и среднеквадратического отклонения. Среднее арифметическое, исходя из которого будет считаться отклонение от показателя равно 160,18 млрд. долл. США.
Показатели дисперсии за период 2007 – 2011 гг. рассчитаны в таблице 3.9. (Приложение 8).
Таблица 3.9.
Расчет показателей дисперсии экспорта и импорта, в млн. долл. США
| Годы | Экспорт/импорт, млрд. долл. | Отклонение | Среднее значение разностей квадратов |
| 115,1 | -45,1 | 2 032 | |
| 149,9 | -10,3 | ||
| 155,6 | -4,6 | ||
| 168,3 | 8,1 | ||
| 212,0 | 51,8 | 2 685 | |
| Итого: | 800,9 | - | 4 910 |
Среднеквадратическое отклонение - обобщающая характеристика размеров вариации признака в совокупности; показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения:
G = 
= 70,1 млрд. долл.
где G - среднее квадратическое отклонение.
Коэффициент вариации используют для сравнительной оценки вариации единиц совокупности и как характеристику однородности совокупности:
V = 
= 
где V - коэффициент вариации.
Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%. По произведенным расчетам можно судить о том, что выборка находится в стандартном пределе отклонения, поэтому целесообразно в следующей главе произвести расчет прогноза экспорта и импорта на 2012 – 2013 гг.
Дата добавления: 2015-07-20; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Исследование состава и структуры импорта, экспорта и инвестиций | | | Экономическое обоснование результатов исследования |