Симметрия

Симметрия — это способ математического описания физических, химических и др. объектов. Симметрия объекта описывается посредством указания перечня операций симметрии { F ₁, F ₂, …}, характерных для данного объекта.

Операция симметрии — процедура, выполняемая над объектом, конечный результат которой в принципе невозможно обнаружить посредством каких-либо экспериментальных наблюдений или измерений.

Другими словами, операция симметрии не оставляет после своего завершения физических последствий в объекте.

Операции симметрии весьма разнообразны. Возьмем объект, находящийся в "стационарном" состоянии и подвергнем его операции сдвига во времени (F = D t), т.е. просто подождем некоторый отрезок времени D t. Если теперь сравнить все измеренные характеристики объекта до и после нашей операции, то мы не найдем никаких отличий. Следовательно, операция сдвига во времени является операцией симметрии, характерной для любых "стационарных" объектов или систем.

Мы можем даже использовать понятие симметрии для определения смысла "стационарности":

Состояние объекта является стационарным, если для него операции сдвигов во времени являются операциями симметрии.

Такой способ классификации состояний и объектов очень эффективен. Во-первых, он является однозначным и объективным. Во-вторых, он дает возможность введения определенной системы классификации объектов (например, на стационарные и нестационарные). Во-вторых, он позволяет ввести ряд количественных характеристик стационарных объектов, например, энергию Е, причем симметрия относительно сдвигов во времени приводит к важному следствию: E = const. Другими словами, из симметрии относительно сдвигов во времени вытекает закон сохранения энергии.

Возьмем теперь "изолированный" объект, т.е. отделенный непроницаемыми границами от окружающей среды и не способный взаимодействовать ни с какими окружающими телами. Все характеристики такого объекта не изменятся при выполнении операций сдвига в пространстве (F = D r) на любое расстояние и в любом направлении и пространственного поворота (F = Dj) на любой угол и вокруг любой пространственной оси. Следовательно, для любых изолированных объектов или систем пространственные сдвиги и повороты являются операциями симметрии. В свою очередь, данные операции симметрии можно использовать для определения смысла "изолированности". Кроме того, они позволяют ввести две важные сохраняющиеся характеристики таких систем — импульс (p = const) и момент импульса (L = const).

Описанные выше операции симметрии часто трактуют как однородность времени, однородность и изотропность пространства.

Знание такой симметрии важно не только в механике, но и в химии. В частности, основные химические объекты — атомы, молекулы, вещества и т.д. обладают всеми описанными операциями симметрии. Это позволяет переносить химическое знание о таких объектах во времени и пространстве. Так, мы можем быть уверены, что химические свойства атома водорода не изменились за последние годы, свойства воды одинаковы в любой лаборатории мира и т.д.

В реальных ситуациях, изучаемые объекты и системы никогда не бывают в точности стационарными или строго изолированными от окружающих тел. Поэтому их симметрия носит более частный характер. При этом существенное значение имеет следующее условие: объект должен быть составным, т.е. должен содержать внутренние части, определенным образом упорядоченные относительно друг друга. Кроме того, хотя бы некоторые из этих частей должны быть одинаковы между собой. Если мы переставим местами две такие одинаковые части, сохраняя общую структуру объекта, то его наблюдаемые характеристики не изменятся при любых условиях (неоднородное окружение, эволюция во времени и т.д.). Такой вид симметрии называется перестановочной.

Возьмем в качестве примера молекулу пропана:

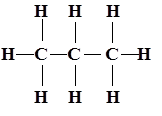
Ясно, что при перестановке местами любых двух атомов углерода (Р _СС) или любых двух атомов водорода (Р _НН), свойства молекулы совершенно не изменятся. Такие перестановки (P_ij) являются операциями симметрии. Напротив, если мы переставим местами атом углерода и атом водорода, то свойства молекулы изменятся чрезвычайно сильно — настолько, что получившаяся молекула не сможет устойчиво существовать и мгновенно разрушится или перегруппируется. Такая перестановка, естественно, уже не будет операцией симметрии.

Заметим, что перестановочные операции симметрии не ограничиваются только бинарными перестановками. В перестановке может участвовать любое число атомов, вплоть до всех атомов, имеющихся в составе молекулы.

Очевидно, что для каждой молекулы мы можем перечислить все возможные перестановки одинаковых атомов, являющиеся операциями симметрии { P_ij }. Такой исчерпывающий список называется группой перестановок ядер молекулы (ГПЯМ). Аналогичные группы существуют и для электронов, входящих в состав атомов и молекул. Они играют важную роль в квантовой химии.

Среди всех перестановок можно выделить некоторые особые, которые можно выполнить посредством глобальных геометрических перемещений всего составного объекта в целом, и в которых сохраняются бинарные соотношения между частицами (например, в молекуле химически связанные атомы остаются связанными, т.е. молекула преобразуется как целое без разрыва химических связей). Перестановки такого специального типа называются пространственными операциями симметрии. Во многих случаях достаточно ограничиться рассмотрением именно этих операций симметрии.

Дата добавления: 2015-07-20