Теоретическое введение

Приложения двойных интегралов

Теоретическое введение

Рассмотрим приложения двойного интеграла к решению ряда геометрических задач и задач механики.

3.1.1 Вычисление площади и массы плоской пластины

Рассмотрим тонкую материальную пластину D, расположенную в плоскости Оху.
Площадь S этой пластины может быть найдена с помощью двойного интеграла по формуле:

­ ­ ­

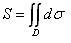
(1)

Пусть в каждой точке пластины задана ее поверхностная плотность γ = γ (x, y) ≥ 0. Будем считать, что функция γ = γ (x, y) непрерывна в области D. Тогда масса m этой пластины равна двойному интегралу от функции плотности γ (x, y) по области D:

­ ­ ­

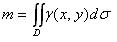
(2)

3.1.2 Статические моменты. Центр масс плоской пластины

Статическим моментом M_x относительно оси Ox материальной точки P (x; y), лежащей в плоскости Oxy и имеющей массу m, называется произведение массы точки на ее ординату, т.е. M_x= my. Аналогично определяется статический момент M_y относительно оси Oy: ­ ­ ­ M_y = mx.
Статические моменты плоской пластины с поверхностной плотностью γ = γ (x, y) вычисляются по формулам:

­ ­ ­

(3)

­ ­ ­

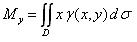
(4)

Как известно из механики, координаты x_c, y_c центра масс плоской материальной системы определяются равенствами:

­ ­ ­

(5)

где m – масса системы, а M_x и M_y – статические моменты системы. Масса плоской пластины m определяется формулой (1), статические моменты плоской пластины можно вычислить по формулам (3) и (4). Тогда, согласно формулам (5), получаем выражение для координат центра масс плоской пластины:

­ ­ ­

(6)

Содержание типового расчета

Типовой расчет содержит две задачи. В каждой задаче задана плоская пластина D, ограниченная линиями, указанными в условии задачи. Г (x,y) – поверхностная плотность пластины D. Для этой пластины найти:
1. S – площадь;
2. m – массу;
3. M_y, M_x – статические моменты относительно осей Оy и Ох соответственно;
4. , 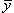– координаты центра масс.

Дата добавления: 2015-07-20