Точка и прямая линия в проекциях с числовыми отметками

Поскольку по одной проекции невозможно определить действительное положение точки в пространстве, то для точек в проекциях с числовыми отметками применяют индексы, определяющие расстояние от точки до плоскости проекции, называемой в проекциях с числовыми отметками плоскостью нулевого уровня (П_О) - Эти индексы, иначе называемые от­метками, пишутся справа и внизу от буквы, обозначающей точку, и могут быть положительными или отрицательными в зависимости от того, нахо­дится точка выше или ниже плоскости нулевого уровня, например А₇, В_-5, С_О (см. рис. 1). Чертежи в проекциях с числовыми отметками обыч­но снабжаются линейным масштабом.

Прямая в проекциях с числовыми отметками может быть задана двумя точками (рис. 2а), или одной точкой, но в этом случае должны быть до­полнительные сведения о направлении убывания отметок и угле наклона прямой к плоскости нулевого уровня (П_О). Эта проблема решается прос­тановкой стрелки, показывающей убывание отметок и величины угла нак­лона данной прямой к плоскости П_О (рис. 2б). Часто вместо угла накло­на оказывается удобнее использовать понятие уклона, уклон обозначает­ся буквой i и определяется как тангенс угла наклона прямой к плоскос­ти П_О. Как видно из рис. 3, уклон прямой СВ будет равен отношению разности величин В₀В₄ и С₀С₄ к величине горизонтальной проекции этой на данной прямой к плоскости П_О (рис. 2б).

Поскольку горизонтальная проекция отрезка (проекция на плоскость П_О) в проекциях с числовыми отметками называется его заложением, а разность отметок начала и конца отрезка называется превышением, то более кратко уклоном отрезка можно назвать отношение его превышения к заложению.

Другим важным понятием, характеризующим прямую в проекциях с чис­ловыми отметками, является понятие интервала. Интервалом называется заложение отрезка данной прямой, у которого разность отметок начала и конца равна единице. Интервал обозначается буквой l. Таким образом, уклон и интервал связаны соотношением i=l/l.

Часто встречающимися задачами, касающимися прямой и точки в про­екциях с числовыми отметками, являются следующие:

1. Градуирование прямой. Под градуированием прямой понимается оп­ределение точек прямой с отметками, выраженными целыми числами и отличающимися друг от друга на единицу длины. Прием градуирования пря­мой показан на рис. 4, здесь возможны два случая:

а. Когда оба конца отрезка имеют одинаковые знаки (рис. 4а,б). В этом случае от конца отрезка с большей отметкой откладывают, перпен­дикулярно к нему, значения разности отметок и проводят графическое градуирование, как показано на рис. 4а. Если концы отрезков имеют дробные отметки, то от конца отрезка с меньшей отметкой откладывают только дробную часть, а от другого - разницу отметок плюс дробную часть отметки конца отрезка. Градуирование при этом выполняют как показано на рис. 46.

б. Случай, когда концы отрезков имеют разные знаки. Построения отличаются лишь тем, что отметки начала и конца отрезка откладываются в противоположные стороны. Пример такого градуирования показан на рис. 4в.

2. Определение взаимного положения отрезков. Во взаимном положе­нии отрезков возможны случаи пересекающихся, скрещивающихся и парал­лельных отрезков. Для того, чтобы определить, пересекаются или скре­щиваются отрезки, достаточно их проградуировать и определить отметки конкурирующих точек, если отметки этих точек одинаковы (точка Е на рис. 5а), то отрезки пересекаются. В том случае, если отметки конку­рирующих точек различны (точки N и Р на рис. 5 б), то отрезки скрещи­ваются.

Выяснение параллельности прямых сводится к проверке следующих ус­ловий:

а. Заложения отрезков параллельны между собой.

б. Направления возрастания - убывания отметок одинаковы.

в. Интервалы (уклоны) отрезков одинаковы. Так отрезки А₄В₁₀ и C₈D₁₄. изображенные на рис. 6, параллельны, если интервал l_ab будет равен интервалу I_cd, так как первые два условия параллельности этих отрезков выполнены.

Рис. 4.

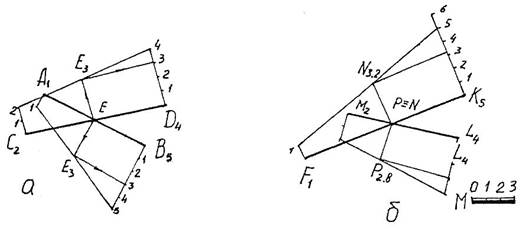
Рис. 5.

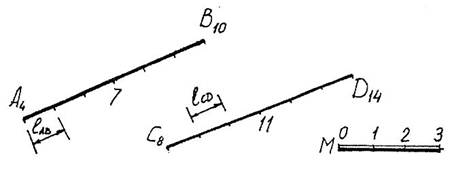
Рис. 6.

Дата добавления: 2015-07-20