
|
Читайте также: |
Задание:
Дана статическая система автоматического регулирования (САР) угловой скорости Она предназначена для стабилизации угловой скорости электродвигателя постоянного тока (Д), входящего в состав лентопротяжного механизма, при различных значениях двух возмущений: напряжения питания и„ и момента нагрузки на валу двигателя Мн . В системе используется принцип регулирования по ошибке.
Задающий элемент представляет собой делитель напряжения (ДН). Значение задающегонапряжения и3 определяет требуемое значение угловой скорости Q.TP при средних значениях напряжения питания ип Ср и момента нагрузки ср-
Функцию датчика регулируемой величины выполняет тахогенератор постоянного тока (ТГ) с математической моделью:
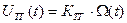 ,
,
где t - время,
 - напряжение на выходе ТГ,
- напряжение на выходе ТГ,
ктг- коэффициент передачи ТГ.
Сравнивающий элемент (СЭ) вырабатывает сигнал ошибки 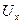 по правилам:
по правилам:
 ,
,
где 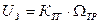 .
.
На выходе сумматора:
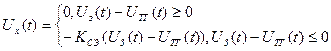
где кСэ - коэффициент передачи СЭ.
Модель усилительно-преобразующего элемента (УПЭ):

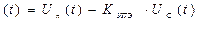
где  - напряжение, подводимое к двигателю,
- напряжение, подводимое к двигателю,
ку - коэффициент усиления УПЭ.
Работа электродвигателя описывается дифференциальным уравнением вида:

где Тм - электромеханическая постоянная времени, 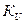 ,
,  - коэффициенты передачи двигателя по напряжению и моменту нагрузки на нулевой частоте.
- коэффициенты передачи двигателя по напряжению и моменту нагрузки на нулевой частоте.
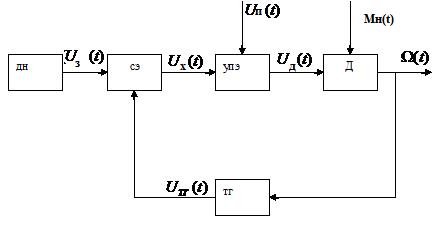
Структурная схема САР угловой скорости
Требуется:
1. Построить структурную модель системы для статического режима работы, вывести формулу для расчета установившегося значения угловой скорости  и найти значение задающего напряжения
и найти значение задающего напряжения  .
.
2. Вычислить абсолютную хст и относительную хст % статические ошибки регулирования для 8 случаев:
а)  ;
; 
б)  ;
; 
в) 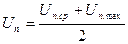 ;
; 
г)  ;
; 
д)  ;
; 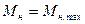
е)  ;
; 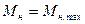
ж) 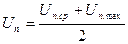 ;
; 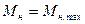
з)  ;
; 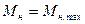
 = F(
= F( ) для 4-х значений
) для 4-х значений  .
. ,
,  .
. по напряжению
по напряжению  ;
;  по
по  ;
;  по
по  ;
;  по
по  .
. и время
и время 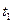 , в момент времени, при котором замыкаются цепи ОС. При
, в момент времени, при котором замыкаются цепи ОС. При  ,
,  .
.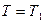 и сделать суждения о времени переходного процесса
и сделать суждения о времени переходного процесса 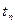 .
.
Дано:

| 
| 
| 
| 
| 
| 
| 
| 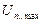
| 
|  
|

| 
| 
| 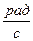
| 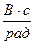
| — | — | 
| 
| 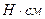
| 
|
| 14,7 | 57,3 | 0,38 | 0,02 | 9,4 | 3,2 | 1,4 | 6,4 |
Решение:
1. Построим структурную модель САР для статического режима и найдем  , обеспечивающее
, обеспечивающее  . При
. При  и
и 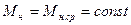 .
.

Коэффициенты:
 - тахогенератора
- тахогенератора
 - сравнивающего элемента
- сравнивающего элемента
 - усилительно-преобразовательного элемента
- усилительно-преобразовательного элемента
 - коэффициент передачи двигателя
- коэффициент передачи двигателя
 - установившееся значение
- установившееся значение
Найдем значение задающего напряжения. Определим из условий:
 ;
;  [H cm]
[H cm]
 ;
;  [B]
[B]
 [
[ 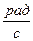 ]
]
Выведем формулу для расчета установившегося значения угловой скорости 
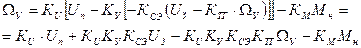


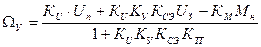
Найдем формулу задающего напряжения:
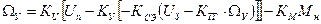 =
=



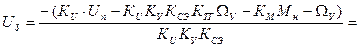


(1)
2. Вычислим абсолютную хст и относительную хст% статические ошибки регулирования для 8 случаев:
а)  ;
; 


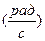
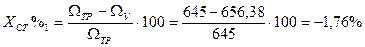
б)  ;
;  ;
;


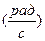 ;
; 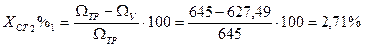 ;
;
в);  ;
; 


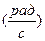 ;
;

г)  ;
;  ;
;
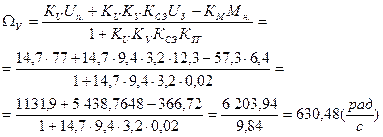


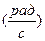
д)  ;
; 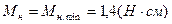 ;
;


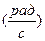
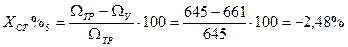
е)  (В);
(В); 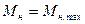 ;
;

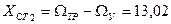
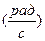

ж) 
 ;
;  (B);
(B);



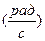
з) 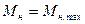 ;
;  .
.

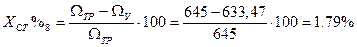

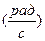
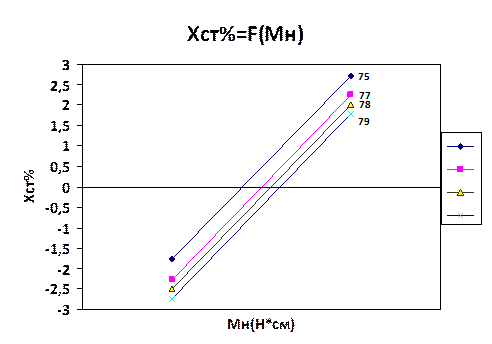
2. По полученным данным построим графики зависимости  дл 4-х значений
дл 4-х значений  .
.

|  6,4 6,4
| ||||||
| Un | 
| Хст, % | Un | 
| Хст, % | ||
| 656,38 | -1,76 | 627,49 | 2,71 | ||||
| 659,6 | -2,26 | 630,48 | 2,25 | ||||
| -2,48 | 631,98 | 2,01 | |||||
| 662,59 | -2,73 | 633,47 | 1,79 |
а) Построим зависимость 
 6,4
6,4
3. Выведем передаточные функции для изображений Лапласа отдельных элементов САР и построим ее структурную модель для динамического режима работы в случае замкнутой цепи ОС.
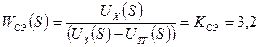



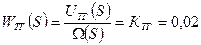
Структурная модель динамического режима в случае замкнутой цепи ОС.

4. Найдем передаточную функцию разомкнутой САР по  :
:  .
.
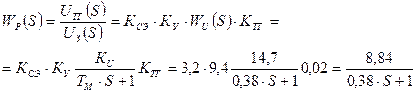
5. Найдем передаточные функции САР:
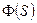 по напряжению
по напряжению  ;
;
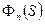 по
по  ;
;
 по
по  .
.
Примем:  ;
;  .
.

Примем:  ;
; 
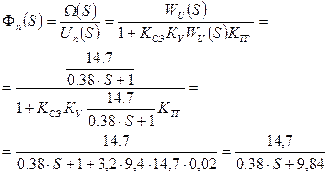
Примем:  ;
;  :
:

7. Найдем дифференциальное уравнение САР для режима пуска при разомкнутой цепи ОС. Математическая модель всей системы совпадает по выражению с математической моделью двигателя.
 ;
;



8. Найдем значение  и времени
и времени 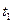 в момент времени, при котором замыкаются цепи ОС.
в момент времени, при котором замыкаются цепи ОС.
При  ,
,  .
.
В момент времени 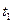 замыкается цепь обратной связи, тогда:
замыкается цепь обратной связи, тогда:
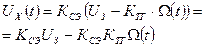 ;
;
При 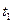 :
: 
 (
(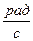 )
)
 ;
; 
 ;
;
 ;
;
 ;
;
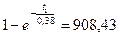 ;
;

9. Найдем дифференциальное уравнение САР на участке после замыкания цепи ОС.
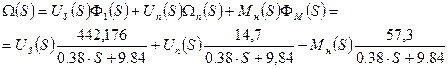 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
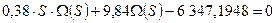 ;
;
С учетом нулевых начальных условий:
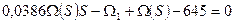
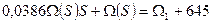

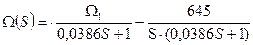
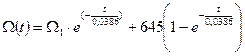

 645+(
645+( -645)
-645) 
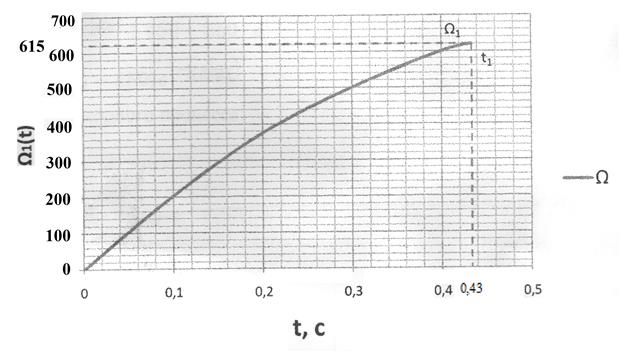
Построим кривую переходного процесса:
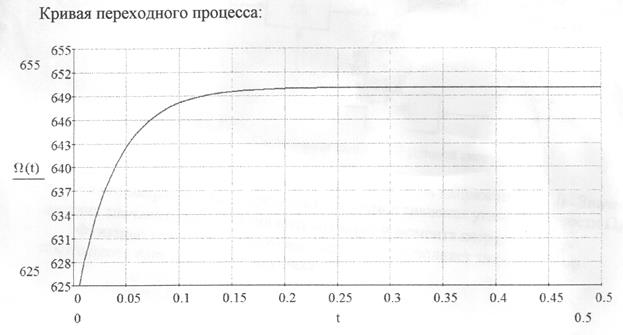
10. Время переходного процесса 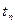 :
:
 , откуда:
, откуда:
 с
с
 c
c
Данная система устойчива, так как в бесконечности процесс стремится к  .
.
Дата добавления: 2015-07-25; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Контрольная работа | | | Темы рефератов |