|
Читайте также: |
Событие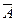 
, состоящее из тех и только тех элементарных исходов опыта, которые не входят в A, называется противоположным событию A.
Несовместные события — события, которые не наступают в одном опыте. Например, противоположные события несовместны.
Вероятности противоположных событий:
; 
.
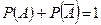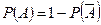Формула сложения вероятностей для совместных событий: Вероятность наступления хотя бы одного из двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного наступления.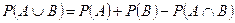 
.
Формула сложения вероятностей для несовместных событий: Вероятность наступления хотя бы одного из двух несовместных событий А и В равна сумме их вероятностей.
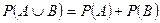
Формула умножения вероятностей для независимых событий: Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей событий А и В.
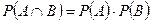
Формула умножения вероятностей для зависимых событий: Вероятность совместного наступления двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого.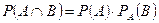 
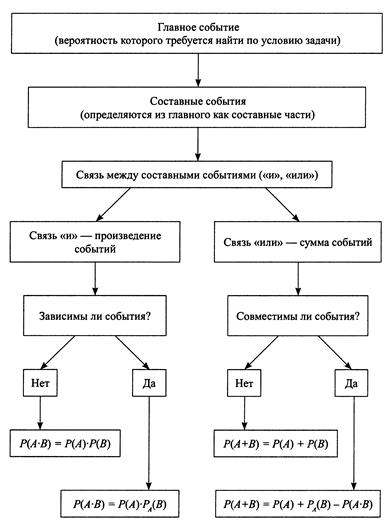
Приведём схему, облегчающую применение формул при решении задач:
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,1. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Решение.
Определим событие A= {выбранная ручка пишет хорошо}.
Тогда противоположное событие 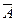= {выбранная ручка пишет плохо}.
Из условия нам известна вероятность противоположного события: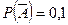 
.
Используем формулу вероятности противоположного события: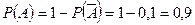 
.
Ответ: 0,9.
10. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Определим события:
A= {вопрос на тему «Вписанная окружность»},
B= {вопрос на тему «Параллелограмм»}.
События A и B несовместны, так как по условию в списке нет вопросов, относящихся к этим двум темам одновременно.
Событие C= {вопрос по одной из этих двух тем} является их объединением: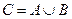 
.
Применим формулу сложения вероятностей несовместных событий: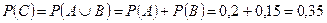 
.
Ответ: 0,35.
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Решение.
Рассмотрим события A = «в автобусе меньше 15 пассажиров» и В = «в автобусе от 15 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,94 = 0,56 + P(В), откуда P(В) = 0,94 − 0,56 = 0,38.
Ответ: 0,38.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
Определим события
A= {кофе закончится в первом автомате},
B= {кофе закончится во втором автомате}.
По условию задачи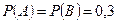 
и 
.
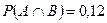По формуле сложения вероятностей найдем вероятность события
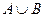= {кофе закончится хотя бы в одном из автоматов}: 
.
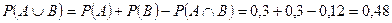Следовательно, вероятность противоположного события {кофе останется в обоих автоматах} равна Р=1-0,48=0,52.
Ответ:0,52.
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Решение.
В этой задаче предполагается, что результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы.
Вероятность каждого попадания равна 0,8. Значит, вероятность каждого промаха равна 1-0,8=0,2. Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что последовательность
A= {попал, попал, попал, промахнулся, промахнулся} имеет вероятность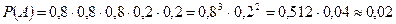 
.
Ответ: 0,02.
В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение.
В этой задаче также предполагается независимость работы автоматов.
Найдем вероятность противоположного события
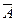= {оба автомата неисправны}.
Для этого используем формулу умножения вероятностей независимых событий: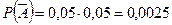 
.
Значит, вероятность события A= {хотя бы один автомат исправен} равна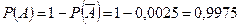 
.
Ответ: 0,9975.
15. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение.
Найдем вероятность противоположного события, состоящего в том, что цель не будет уничтожена за n выстрелов. Вероятность промахнуться при первом выстреле равна 0,6, а при каждом следующем — 0,4. Эти события независимые, вероятность их произведения равна произведению вероятности этих событий. Поэтому вероятность промахнуться при n выстрелах равна: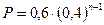 
. Осталось найти наименьшее натуральное решение неравенства 
; 
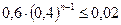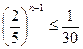. Последовательно проверяя значения n, равные 1, 2, 3 и т. д. находим, что искомым решением является n =5. Следовательно, необходимо сделать 5 выстрелов.
Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов:
Р(1) = 0,6.
Р(2) = Р(1)·0,4 = 0,24.
Р(3) = Р(2)·0,4 = 0,096.
Р(4) = Р(3)·0,4 = 0,0384;
Р(5) = Р(4)·0,4 = 0,015536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени.
Ответ: 5.
16. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
Решение.
Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: Р=0,5·0,5·0,5 = 0,125.
Другой способ решения:
Т.к. жеребьёвку можно рассматривать как подбрасывание монеты, то задачу можно решить по технологии решения задач с монетами. Жеребьёвка проводилась три раза, поэтому N=23=8. Присвоим элементарному событию ««Статор» начинает игру» значение «Орел». Тогда благоприятный исход соответствует только комбинации «ОРО», т.е. N(A)=1. Поэтому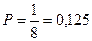 
Ответ: 0,125.
17. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 3 группы, по 7 человек в каждой. Найти вероятность того, что Аня и Нина окажутся в одной группе.
Решение.
Подруги могут оказаться вместе в любой из трёх групп. Рассмотрим некоторую одну группу. Вероятность того, что Аня окажется в ней, равна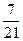 
. Если Аня уже находится в этой группе, то вероятность того, что Нина окажется этой же группе равна 
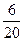. Тем самым, вероятность того, что обе подруги окажутся в этой группе, равна 
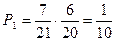. Такой же будет вероятность того, что Аня и Нина окажутся во второй группе или третьей группе. Эти события несовместны, тогда искомая вероятность равна сумме вероятностей этих событий: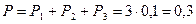 
Ответ: 0,3.
В следующих задачах для решения удобно использовать дерево вероятностей. В части задач дерево построено прямо в условии. В других задачах это дерево следует построить.
18. Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно.
Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку G.
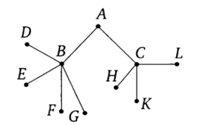
Решение.
Схема дорожек представляет собой граф, а именно — дерево. Рёбра (ветви) дерева соответствуют дорожкам. Около каждого ребра напишем вероятность того, что Павел Иванович пройдет по соответствующей дорожке. Выбор пути на каждой развилке происходит наудачу, поэтому вероятность поровну делится между всеми возможностями. Предположим, что Павел Иванович пришел в вершину C. Из неё выходит три ребра CH, CK и CL. Следовательно, вероятность того, что Павел Иванович выберет ребро CH, равна 1/3. Аналогично можно расставить все вероятности.
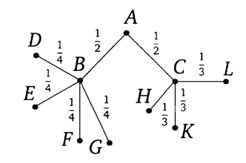
Каждый маршрут из начальной точки A в любую из конечных точек является элементарным событием в этом эксперименте. События здесь не равновозможные. Вероятность каждого элементарного события можно найти по правилу умножения.
Нам нужно найти вероятность элементарного события
G= {Павел Иванович пришел в точку G}.
Это событие состоит в том, что Павел Иванович прошел маршрутом ABG. Вероятность находится умножением вероятностей вдоль ребер AB и BG: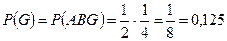 
.
Ответ: 0,125.
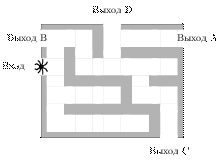
19. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу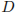 
.
Решение.
На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625.
Ответ: 0,0625.
Рассмотрим задачу, обобщающую условия целого ряда вероятностных задач, решаемых с помощью дерева вероятностей.
В некотором эксперименте вероятность события A равна 0,3. Если событие A наступает, то вероятность события C равна 0,2, а в противоположном случае вероятность события C равна 0,4. Найдите вероятность события C.
Решение.
В таких задачах удобно изобразить эксперимент графически деревом вероятностей. Отличие от предыдущих задач состоит в том, что вероятности на ребрах получаются не из равновозможности, а иначе.
Весь эксперимент обозначим буквой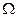 
(большая омега) и поставим точку около этой буквы — корень дерева, из которого ветви-ребра растут вниз. Из точки 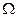проведем ребро вниз-влево в точку A. Событие A имеет вероятность 0,3, поэтому подпишем у этого ребра вероятность 0,3. Противоположное событие 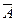имеет вероятность 0,7. Проведем второе ребро в точку .
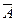Если осуществилось событие A, то событие C по условию имеет вероятность 0,2. Поэтому из точки A проведем ребро вниз-влево в точку C и подпишем вероятность. Действуя так же и дальше, достроим все дерево (см. рис.).
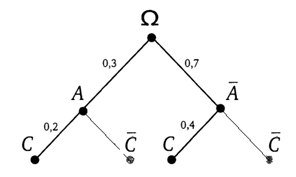
Чтобы найти вероятность события C, нужно выделить только те пути, которые ведут из корневой точки 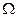к событию C. На рисунке эти пути яркие, а пути, не приводящие к C, изображены бледно. Выделенные пут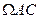и 
и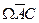 
являются элементарными событиями, благоприятствующими событию C.
Теперь нужно вычислить вероятности выделенных путей и сложить их. Пользуясь правилами умножения и сложения вероятностей, получаем:
.
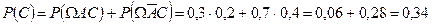Ответ: 0,34.
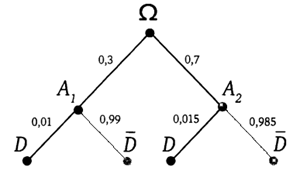
20. Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает 30% всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, 1% имеют скрытые дефекты, а у выпускаемых второй фабрикой —1,5%. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
Решение.
Введем обозначения для событий:
A1= {телефон выпущен на первой фабрике},
A2= {телефон выпущен на второй фабрике},
D= {телефон имеет скрытый дефект}.
По условию задачи составим дерево и найдём необходимые вероятности.
.
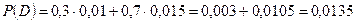Ответ: 0,0135
21. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства —20% яиц высшей категории. Всего высшую категорию получает 35% яиц из этих двух хозяйств. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение.
Эта задача является обратной к предыдущей. Событие «яйцо имеет высшую категорию» назовем H. События «яйцо поступило из первого хозяйства» и «яйцо поступило из второго хозяйства» назовем A1 и A2 соответственно. Обозначим буквой p искомую вероятность события A1 и нарисуем дерево.
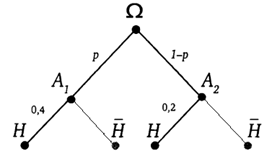
Получаем: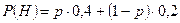 
.
По условию эта величина равна 0,35.
Тогда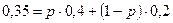 
,
откуда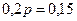 
и, значит, 
.
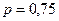Ответ: 0,75.
22. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение.
По условию задачи составим дерево и найдём необходимые вероятности.
|
|
|
|
 |  |  |  | ||||||||
|
|
Джон промахнется, если: А) схватит пристрелянный револьвер и промахнется из него, или если В) схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно Р(А)= 0,4·(1 − 0,9) = 0,04 и Р(В)=0,6·(1 − 0,2) = 0,48. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий. Тогда искомая вероятность равна Р=0,04 + 0,48 = 0,52.
Ответ: 0,52.
23. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение.
По условию задачи составим дерево и найдём необходимые вероятности.
|
|
|
|
  |   |   |   | ||||||||
|
|
Анализ пациента может быть положительным по двум причинам: А) пациент болеет гепатитом, его анализ верен; B) пациент не болеет гепатитом, его анализ ложен. Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем:
; 
;
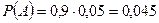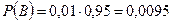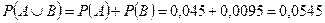
Ответ: 0,0545.
24. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение.
По условию задачи составим дерево
|
3 июля
|
|
|
4 июля
 |  |  |  |
|
|
|
|
|
|
| |||||||
| |||||||||
5 июля
 |  | ||||||||||||||
 |  |  |  |  | |||||||||||
| |||||||||||||||
|
|
|
|
|
|
|
|
Для погоды на 4, 5 и 6 июля есть 4 варианта (здесь Х — хорошая, О — отличная погода): (А) ХХО, (В) ХОО, (С) ОХО, (D) ООО. Найдем вероятности наступления такой погоды:
P(A) = 0,8·0,8·0,2 = 0,128;
P(B) = 0,8·0,2·0,8 = 0,128;
P(C) = 0,2·0,2·0,2 = 0,008;
P(D) = 0,2·0,8·0,8 = 0,128.
Указанные события несовместные, вероятность их сумы равна сумме вероятностей этих событий:
P= 0,128 + 0,128 + 0,008 + 0,128 = 0,392.
Ответ: 0,392.
Дата добавления: 2015-07-25; просмотров: 170 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка. | | | ВВЕДЕНИЕ |