Сообщения OSPF

Тип сообщения Hello - Это основной тип сообщений.

Для рассылки используется групповой адрес 224.0.0.5 (ALL-OSPF-Routers).

Выполняет следующие функции:

· Поиск соседних маршрутизаторов.

· Выбор маршрутизаторов DR и BDR.

· Определение статуса канала.

· Установление партнерских отношений между маршрутизаторами.

Тип сообщения Database Description - Маршрутизаторы обмениваются данными из баз данных OSPF.

Тип сообщения Link State Request -Запрос части базы данных для обновления.

Тип сообщения Link State Update - Передача части базы данных, которая была запрошена.

Тип сообщения Link State Acknowledgment - Используется для подтверждения получения фрагмента базы данных.

Уведомление о состоянии канала - Link State Advertisement (LSA)

Сводная информация о каналах к сетям, рассылает граничный маршрутизатор области ABR внутри своей области.

Сводная информация о канале к граничному маршрутизатору автономной системы ASBR, рассылается граничным маршрутизатором области ABR внутри своей области.

Маршрутная таблица OSPF содержит в себе:

· IP-адрес места назначения и маску;

· тип места назначения (сеть, граничный маршрутизатор и т.д.);

· тип функции (возможен набор маршрутизаторов для каждой из функций TоS);

· область (описывает область, связь с которой ведет к цели, возможно несколько записей данного типа, если области действия граничных маршрутизаторов перекрываются);

· тип пути (характеризует путь как внутренний, межобластной или внешний, ведущий к AS);

· цена маршрута до цели;

· очередной маршрутизатор, куда следует послать дейтограмму;

· объявляющий маршрутизатор (используется для межобластных обменов и для связей автономных систем друг с другом).
Подключится к демону OSPF, можно с помощью telnet по порту 2604, и просмотреть базу.

Реальная база OSPF. Видно, что только одна область (0.0.0.0).

ADV Router - Advertising router, который породил LS.

2.4 Выбор кратчайших путей.

Большинство сетей с коммутацией пакетов (сообщение разбивается на пакеты фиксированной длины, которые передаются независимо друг от друга, а затем собираются в исходное сообщение приёмником) осуществляют маршрутизацию на сетевом уровне модели OSI с применением различных алгоритмов выбора оптимального пути. Большинство алгоритмов основано на учете меры «стоимости» («сложности»), приписываемой каждой линии и/или каждому узлу. «Сложность» может быть фиксированной и учитывать такие параметры, как длина линии, скорость передачи, безопасность, величина нагрузки на линию, время задержки. «Сложность» может зависеть от вида входящей нагрузки и динамически изменяться с изменением вышеперечисленных параметров. Выбор маршрутов может выполняться централизовано, в узле управления сетью, а затем полученная информация рассылается по всем узлам. Децентрализованный выбор маршрутов предполагает обмен информацией между узлами о сложности и маршрутах до тех пор, пока в узлах не сформируются таблицы маршрутов с необходимыми данными о кратчайших путях.

Рассмотрим работу алгоритма централизованного выбора на примере сети (рис. 1). Для реализации алгоритма требуется знание глобальной структуры сети, т. е. списка всех узлов, и “cложности” линий связи. В примере на рис. 1. Целью является нахождение кратчайш их пут ей от узла 1, являющегося источником, ко всем остальным узлам сети. Алгоритм решает эту задачу поэтапно, строя дерево кратчайших путей от узла 1 ко всем остальным узлам. На k -м шаге вычисляются кратчайшие пути к k -узлам, ближайшим к источнику. Эти узлы включаются во множество узлов N уже охваченных алгоритмом.

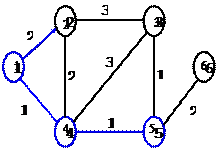
Обозначим через D(v) расстояние (как сумму cложностей) от начального узла (1) до узла V. Пусть l(i,j) - заданная cложность пути между узлами I и J. Алгоритм состоит из двух частей: начального шага и итераций, повторяющихся до завершения алгоритма.

1. Начальный шаг. Устанавливаем N={1}. Для каждого узла V, не принадлежащего множеству N, устанавливаем D(v)=l(1,v)- cложность от узла 1 до узла v. Расстояние до узлов, не соединенных с узлом 1, принимаем бесконечно большим и обозначается “-“.

2. Каждый последующий шаг. Находим не принадлежащий множеству N узел W, для которого cложность D(w) минимальна и включаем W во множество N {}. Затем обновляем значения D(w) для всех остальных узлов не принадлежащих N путем вычисления

,

находится минимальное значение из:

- D(w)=l(1, w)- cложности от узла 1 до узла w (напрямую);

- D(v)+ l(w, v)= l(1, v) + l(w, v) - cложности от узла 1 до узла w (через узел v).

Шаг 2 повторяется, пока во множество N не войдут все узлы. На каждом шаге во множество N добавляется станция, имеющая минимальную cложность от начального узла. Применение алгоритма к сети иллюстрируется последовательными шагами, указанными в таблице. В столбцах полужирным шрифтом обозначены и выделены цветом минимальные значения D(w) на каждом шаге. При равных расстояниях выбор производится случайно. После каждого шага соответствующий узел W (с минимальной “cложностью”) добавляется к множеству N, величины D(w) обновляются.

Например, после начального шага к множеству N добавляется узел 4 имеющий минимальное значение D(4)=1. На шаге 3 к множеству N добавляется узел 5 c минимальной сложностью D(5)=2 (т.к.D(3)=4, D(5)=2 и D(5)<D(3)) и т.д. После шага 6 алгоритм завершает свою работу.

На каждом шаге cложность определяется (вычисляется) от начальной станции до всех других (столбцы D(2) – D(6)). В столбце N при этом указывается не путь, а множество станций, до которых уже найдены пути с минимальными cложностями. D(N)- сложность до станции, выбранной на данном шаге в столбец N от начального узла.

По мере работы алгоритма строится дерево кратчайших путей с корнем в узле 1. С помощью дерева можно получить таблицу маршрутов для узла 1, показывающую пути, по которым нужно направлять сообщения к узлам назначения. Таблица 1.

Шаг	Маршрут	N	D(N)	D(2)	D(3)	D(4)	D(5)	D(6)
Нач.	-	{1}			--		--	--
	{1,4}	{1,4}			4=1+3		2=1+1	--
	{1,4,5}	{1,4,5}			3=1+1+1			4=1+1+2
	{1,2}	{1,2,4,5}
	{1,4,5,3}	{1,2,3,4,5}
	{1,4,5,6}	{1,2,3,4,5,6}

Шаг «Нач». Шаг 2. Шаг 3. Шаг 4. Шаг 5. Шаг 6.

3. Задание на лабораторную работу

3.1. Изучить теоретический материал и ответить на контрольные вопросы.

3.2.

Составить таблицу маршрутизации (см. табл.1) для своего узла в соответствии с рис. 1. Номер узла равен номеру вашего компьютера. Если номер компьютера больше 6 или равен 1, то необходимо к рис. 1 пририсовать ещё один узел, имеющий несколько связей (>1) с другими узлами, проставить cложности до этого узла произвольным образом и составить таблицу маршрутизации для этого узла в соответствии с полученным рисунком. Сложности на рисунке 1 - не менять.

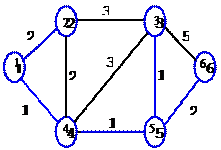Чтобы было проще разобраться в задании 3.2 проведите следующую последовательность действий:

Дата добавления: 2015-07-25