Маятника максвелла

ЛАБОРАТОРНАЯ РАБОТА №6

ИССЛЕДОВАНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ

И ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ

МАЯТНИКА МАКСВЕЛЛА

Оснащение прибора: Маятник Максвелла, комплект заменных колец с указанием массы, миллисекундомер.

Вращательным называют такое движение, при котором все точки твердого тела движутся по окружности, центры которых расположены на одной прямой, называемой осью вращения. Конечно, предполагается, что вращение рассматривается в некоторой определенной системе отсчета. Если в этой системе отсчета ось вращения неподвижна, то говорят, что тело вращается около неподвижной оси. Очевидно, все точки, находящиеся на оси вращения, будут в данной системе неподвижны. Если ось вращения в выбранной системе сама движется, то говорят, что тело вращается около движущейся оси. Например, вращение цилиндра, катящегося по плоскости (рис. 1.), можно рассматривать относительно покоящейся системы отсчета К, связанной с плоскостью качения, или относительно поступательно движущейся системы К’, жестко связанной с осью цилиндра. В системе отсчёта К вращение тела происходит относительно оси цилиндра,

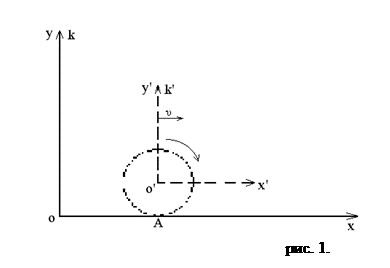которая сама перемещается в пространстве. В системе же К` ось вращения (ось цилиндра) неподвижна.

Для сложных движений вводится понятие мгновенной оси вращения. Мгновенная ось представляет собой совокупность точек тела, имеющих в данной момент скорость, равную нулю, относительно основной (неподвижной) системы отсчёта К`. Положение мгновенной оси вращения в системе К с течением времени изменяется: но в каждый отдельный момент ось неподвижна. Это возможно, если положение оси вращения меняется относительно самого тела. В примере с цилиндром (рис. 1.) мгновенной осью является совокупность точек, в которых цилиндр касается плоскости (на рис. 1. это прямая, проходящая через точку А перпендикулярно чертежу). Движение цилиндра в данный момент времени есть простое вращение его около мгновенной оси. Очевидно, что в другой момент времени в соприкосновение с плоскостью придут другие точки цилиндра, а это значит, что мгновенная ось будет проходить через другие точки движущегося цилиндра. В дальнейшем ось вращения пройдет через новые точки цилиндра и т.д.

При неподвижной оси вращения все точки твердого тела движутся по окружностям, расположенным в плоскостях, перпендикулярных к оси вращения. Известно, что движение точки по окружности может быть описано как линейными характеристиками (дуговой координатой S, Линейной скоростью V, линейным ускорением а), так и угловыми (угол поворота φ, угловой скоростью ω и угловым ускорением β).

Так как линейные кинематические характеристики движения точек зависят от их расстояния до оси вращения, то они не могут служить характеристиками вращательного движения тела как целого. С другой стороны, угловые характеристики (φ,ω,β) для всех точек твердого тела должны быть одинаковы, иначе точки сместились бы по отношению друг к другу, что для абсолютно твердого тела невозможно. Таким образом, угол поворота φ, угловая скорость ω и угловое ускорение β, взятые для какой-либо одной точки, будут в то же время характеризовать вращение тела как целого.

Если тело имеет неподвижную ось, т.е. закреплённую в неподвижных подшипниках, то при любой системе действующих сил тело может вращаться лишь около этой оси.

Но не всякая сила может вызвать вращение. Например, сила, параллельная оси (F_II)

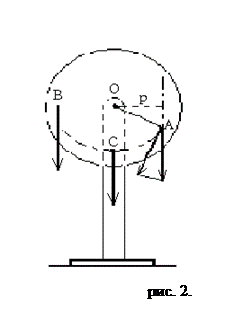
не вызовет вращения; она лишь стремиться сдвинуть тело вдоль оси и в конечном счете уравновешивается реакцией подшипников. Но вот сила. находящаяся в плоскости, перпендикулярной к оси, может при некоторых условиях вызвать вращение. Выясним эти условия на опыте с диском, который может вращаться около горизонтальной оси Z (точка О на рис. 2.) В точке А диска прикрепим груз массой т. Сила 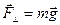лежит в плоскости диска. Опыт покажет, что диск под действием силы 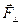начнет поворачиваться по часовой стрелке. Если груз поместить на другую сторону диска (в точке В), то вращение будет происходить в противоположную сторону. Когда же сила 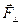будет приложена в точке С, лежащей на вертикали, которая проходит через ось, вращение не возникнет. Если ввести понятие момента силы М_z относительно оси вращения в виде векторного произведения

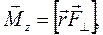(1)

где 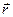- вектор, соединяющий в плоскости действия силы ось с точкой приложения силы 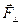, то станет понятным, то вращение вызывают только такие силы 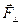, момент которых относительно оси вращения Z не равен нулю.

Вектор 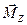считается направленным по оси вращения в сторону, определяемую правилом векторного произведения или правилом правого винта: если вращать головку винта, ориентированного вдоль оси Z, в направлении действия силы, то поступательное движение его укажет направление момента .

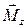В случае, когда на тело действуют несколько сил, результирующий момент равен векторной сумме моментов отдельных сил. Но так как все эти векторы направлены по одной оси Z, то векторная сумма может быть заменена алгебраической. При этом надо считать положительными те моменты, которые вызывают тела по часовой стрелке, и отрицательными, если они вызывают вращение против часовой стрелки. Модуль момента силы согласно (1) равен:

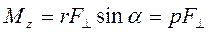
где величину 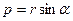называют плечом силы 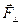(это кратчайшее расстояние между осью вращения и направлением действия силы 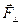). Для вектора момента силы можно записать следующую формулу:

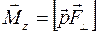(1`)

С другой стороны, (1) можно записать и так:

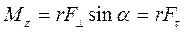(2)

где 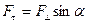проекция силы 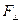в направлении, перпендикулярном вектору r (эта составляющая направлена по касательной к окружности, по которой движется точка приложения силы 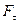). Величину 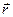называют в этом случае плечом силы 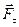. Из (2) следует еще одно векторное выражение для момента силы :

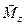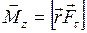(2`)

Из изложенного видно, что вектор момента силы 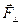можно представить тремя способами:

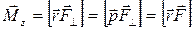(3)

Если не тело действует сила, ориентированная произвольно, то её следует разложить на две составляющие: составляющую, параллельную оси (она момента не создает), и составляющую 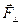, лежащую в плоскости, перпендикулярной оси Z. (Эта составляющая создает момент 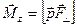.) Можно, конечно, разложить силу и на три составляющие: по оси Z, по радиусу 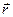(они не создают момента) и составляющую 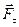, перпендикулярную 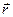и лежащую в плоскости, перпендикулярной оси Z; последняя создает момент .

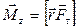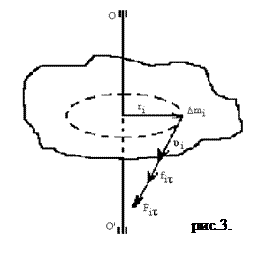
Тело произвольной формы с закреплённой в подшипниках осью О`O` (ось Z на рис. 3.) мысленно разобьём на малые элементы (точки) массой 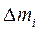. Все эти элементы при вращении тела около неподвижной оси Z будут двигаться по окружностям, расположенным в плоскостях, перпендикулярных к оси. Обозначим радиусы этих окружностей через 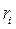. Предположим, что на каждый элемент тела действует внешняя сила 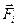и сила внутреннего происхождения 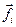. Так как движение элементов тела происходит по плоским окружностям с тангенциальным ускорением 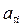, то значение имеет не сами силы 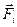и 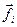, а только их составляющие 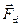, , 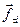направленные по касательным к этим окружностям.

Запишем для элемента i – го номера второй закон Ньютона (в проекции на касательную к окружности):

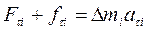(4)

Умножая обе части этого равенства на радиус 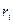окружности, описываемой элементом массы, и вводя вместо тангенциального угловое ускорение β, одинаковое для всех элементов (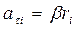), получим:

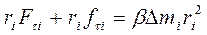
Но 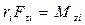есть вращательный момент внешней силы, а 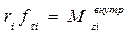- момент внутренней силы.

Суммируя вращающие моменты, приложенные ко всем элементарным массам, составляющим тело, и учитывая, что сумма моментов внутренних сил равна нулю, получим:

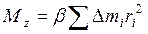, (5)

где 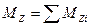- суммарный момент внешних сил, приложенных к телу.

Произведение массы материальной точки на квадрат ее расстояния от оси вращения

называют моментом инерции материальной точки относительно оси и обозначают через :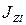

.

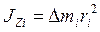Для данного тела и заданной оси вращения сумма

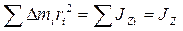(6)

есть величина постоянная; её называют моментом инерции тела относительно заданной оси Z.

Таким образом, момент инерции тела относительно некоторой оси называют сумму моментов инерции (относительно той же оси) всех материальных точек, составляющих тело. Очевидно, в системе СИ единицей момента инерции является 1 .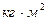

Маятник Максвелла предназначен для исследования закона сохранения энергии и определении на этом основании момента инерции металлических колец.

Параметры маятника Максвелла:

Диаметр оси маятника D₀ – 10мм

Внешний диаметр D_р – 86мм

Внешний диаметр колец D_к – 105 мм

Диаметр нити подвески D_н – 0.5 мм

Дата добавления: 2015-07-25