
1. Продовжить формулювання:
„Функція  називається обмеженою з обох сторін або просто обмеженою на множині {x}, якщо...”.
називається обмеженою з обох сторін або просто обмеженою на множині {x}, якщо...”.
2. Встановити, якою є функція  (неперервною чи розривною)
(неперервною чи розривною)
для кожного з заданих значень аргументу  .
.
1. при х=5 функція неперервна, х=3 – розрив ІІ-го роду.
2. при х=3 функція неперервна, х=5 – розрив ІІ-го роду.
3. при х=3 функція неперервна, х=5 – розрив І-го роду.
4. при х=3, х=5 – розриви ІІ-го роду.
3. Обчислити границі з невизначеністю типу  та
та  :
:
а) 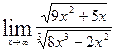 ; б)
; б) 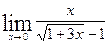
1. а) 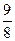 б) б) 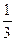
| 2. а)  ; б) 1 ; б) 1
| 3. а)  ; б) ; б) 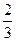
| 4. Інша відповідь |
4. Обчислити границі із застосуванням першої та другої цікавих границь а) 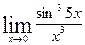 ; б)
; б) 
1. а) 125; б) 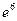
| 2. а) 3; б) 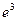
| 3. а) 5; б) 
| 4. Інша відповідь |
Дата добавления: 2015-07-25; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тест № 11 | | | Тест № 13 |