Индивидуальное Домашнее Задание №2 по теме

«Механические колебания. Решение олимпиадных задач». 2013 г.

Задание выполняется в тетради в клеточку (не менее 18 листов). Решение каждого задания начинается с нового листа. Обязательно перед началом решения должно быть записано (или приклеено) полное условие задачи. Следует также оставить место для замечаний преподавателя и записи нового решения. Должна соблюдаться заданная последовательность заданий. Если вы не смогли решить какую-либо задачу, то все равно нужно выписать ее условие и оставить место (хотя бы 1 страницу) для последующего решения.

Решения задач должны быть записаны аккуратно, оно должно быть подробным со всеми необходимыми рисунками, пояснениями и алгебраическими выкладками.

Срок выполнения задания. 21 октября – 18 ноября.

Часть 1.

1. Груз колеблется по вертикали на резиновом шнуре с частотой n₁. Чему будет равна частота вертикальных колебаний n₂ груза, если его подвесить на том же шнуре, сложенном вдвое? (2002)

2. Однородную по длине пружину жесткости k разрезали на две части так, что отношение их длин равно n. С помощью получившихся двух пружин небольшое тело массы m закрепили между двумя стенками так, что обе пружины оказались недеформированными (см. рис.). Пренебрегая массой пружин и силой тяжести, найдите период малых колебаний данного тела. Влияние силы трения не учитывать (1997)

3. Металлический стержень длины L = 1 м подвешен за середину к пружине (см. рис.). Стержень совершает вертикальные гармонические колебания с амплитудой A = 10 см и максимальным ускорением a = 10 м/с² в однородном магнитном поле с индукцией B = 0,01 Тл, направленном перпендикулярно плоскости колебаний. Определите максимальную разность потенциалов U, возникающую на концах стержня. (2002)

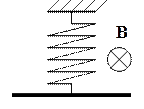
4. Найдите период малых вертикальных колебаний тела массы m в системе, показанной на рисунке, если точка подвеса верхней пружины движется вниз с постоянным ускорением a < g, где g – ускорение свободного падения. Жесткости пружин равны k₁ и k₂, а их массы пренебрежимо малы. (2003 - 2005)

5. Жидкость объемом V налита в изогнутую трубку с площадью поперечного сечения S. Одно колено трубки вертикально, а другое составляет угол a с вертикалью (см. рис.). Пренебрегая вязкостью, найдите период малых колебаний жидкости в трубке. (1999, 2002)

6. Колебательная система состоит из двух шариков, массы которых m₁ = 2m и m₂ = m, прикрепленных к концам невесомой пружины. Если закрепить неподвижно первый шарик, то циклическая частота колебаний второго равна w₂. При закреплении второго шарика циклическая частота колебаний первого равна w₁. Найдите циклическую частоту колебаний системы, когда оба шарика не закреплены, если пружину сжать на некоторую величину и отпустить. Колебания происходят в горизонтальной плоскости только вдоль пружины. Трение не учитывать. (2005, 2006)

7. Коробка массы M стоит на горизонтальном столе. В коробке на пружине жесткости k подвешен груз массы m (см. рис.). При какой амплитуде колебаний груза m коробка начнет подпрыгивать на столе? (2002, 2003)

8. Коробка массы M стоит на горизонтальном столе. Коэффициент трения между столом и коробкой равен m. Внутри коробки лежит груз массы m, который может без трения двигаться по дну коробки (см. рис.). Он прикреплен к стенке коробки пружиной жесткости k, которая в положении равновесия не напряжена. При какой амплитуде колебаний груза коробка начнет двигаться по столу? (2002, 2003)

9. Определите максимальную амплитуду гармонических колебаний системы, состоящей из двух брусков и двух невесомых пружин, при которой бруски будут совершать колебания по горизонтальной плоскости без проскальзывания относительно друг друга (см. рисунок). Жесткость пружин 2k и 4k.

Масса нижнего бруска 2m, верхнего – m, коэффициент трения между брусками равен m. В положении равновесия пружины не деформированы. Трение между нижним бруском и плоскостью отсутствует. (2002 - 2005)

10. Определите максимальную амплитуду гармонических колебаний системы, состоящей из трех брусков и двух невесомых пружин, при которой бруски будут совершать колебания по горизонтальной плоскости без проскальзывания относительно друг друга. Жесткость пружин 2k и 3k.

Масса нижнего бруска 3m, среднего бруска – 2m, верхнего – 5m; коэффициент трения между нижним и средним брусками m, а между средним и верхним – 2m. В положении равновесия пружины не деформированы. Трение между нижним бруском и плоскостью отсутствует. (2006)

Часть 2.

11. К маятнику АВ с шариком массы 2m подвешен маятник ВС с шариком массы 3m. Точка A совершает колебания в горизонтальном направлении с периодом Т. Определите длину L нити ВС, если известно, что нить АВ все время остается вертикальной (1993, 2006).

12. К пружине жесткости k прикреплена горизонтально расположенная проводящая перемычка AB длины L и массы m, которая может скользить по неподвижным вертикальным проводящим рельсам AK и BP без нарушения контакта. Рельсы замкнуты на батарею конденсаторов, емкости которых указаны на рисунке. Система находится в однородном магнитном поле с индукцией B, направленной в горизонтальной плоскости перпендикулярно перемычке. Найдите частоту вертикальных колебаний перемычки. Электрическим сопротивлением, индуктивностью элементов системы и силами трения пренебречь.

(1997, 2003 – 2006)

13. Система, состоящая из пружины, поршня и столба жидкости длиной L, выведена из состояния покоя и затем совершает свободные малые колебания (см. рис.). Пренебрегая трением, определите массу поршня, если период этих колебаний равен T, площадь поперечного сечения трубы S, плотность жидкости r, жесткость пружины равна k. (1993, 2001, 2003)

14. Четыре одинаковых шарика массы 2m каждый, соединенные пружинами жёсткости k, образуют квадрат. Одновременно все четыре шарика толкнули, сообщив им одинаковые по модулю скорости, направленные к центру квадрата. Через какое минимальное время после этого пружины будут сильнее всего растянуты? Массами пружин пренебречь. (1998, 2002 – 2006)

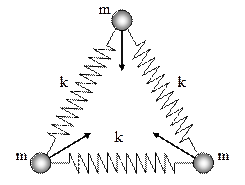
15. Три одинаковых шарика массы m каждый, соединенные пружинами жёсткости k, образуют равносторонний треугольник (см. рис.). Одновременно все три шарика толкнули, сообщив им одинаковые по модулю скорости, направленные к центру треугольника. Через какое время после этого пружины будут сильнее всего растянуты? Массами пружин пренебречь. (2002 - 2006)

16. Шесть одинаковых шариков массы m каждый, соединенные пружинами жёсткости 2k, образуют правильный шестиугольник (см. рис.). Одновременно все шесть шарика толкнули, сообщив им одинаковые по модулю скорости, направленные к центру шестиугольника. Через какое время после этого пружины будут сильнее всего сжаты? Массами пружин пренебречь. (2002 – 2006)

17. Тонкий поршень массы m расположен в равновесии посредине гладкого горизонтального цилиндрического сосуда диаметра D и длины L. По обе стороны от поршня находится идеальный газ, давление которого равно p ₀. Если поршень сместить из положения равновесия на малое расстояние а (a << L) и затем отпустить, то он начнет совершать гармонические колебания. Определите время, за которое при колебаниях поршень сместится из положения равновесия на расстояние, равное 0,5 a. Трение не учитывать. Процесс считать изотермическим. (2003, 2004)

18. Тонкая, открытая с обоих концов трубка, согнутая под углом a расположена в вертикальной плоскости (см. рис.). Верхнее колено трубки заполнено на длину L жидкостью, которая удерживается с помощью клапана K. Найдите, через какое время t после открывания клапана, вся жидкость вытечет из горизонтальной части трубки, длина которой равна 2L. Силами трения и поверхностного натяжения пренебречь. При течении жидкость заполняет всё сечение трубки. Решите задачу для a = 60°, 90°, 150°. (2002 - 2006)

19. Трос длины L движется по инерции внутри горизонтальной трубы, которая изгибается в вертикальной плоскости под углом a = 30°. Когда трос, поднимаясь по трубе, остановился, в наклонной части трубы оказалась половина его длины. Определите, сколько времени прошло от начала подъема троса до момента, когда в наклонной части трубы оказалась четвертая его часть. Силами трения пренебречь. (2005, 2006)

20. Стержень длины L совершает малые колебания вокруг горизонтальной оси, проходящей через точку O. Середина стержня опирается на пружину жесткости k. На стержне закреплены два маленьких груза массы m и 2m, положения которых показаны на рисунке. Найдите период колебаний стержня, если в положении равновесия он расположен горизонтально. Массами пружины, стержня, а также силами трения пренебречь. (2004 - 2006)

21. Стержень длины L с закрепленными на концах грузами массы 2 m и 3 m совершает малые колебания вокруг горизонтальной оси, проходящей через точку O, и отстоящую на длину L /4 от его верхнего конца. В точке C, на расстоянии L /4 от оси, стержень соединен с пружиной жесткости k. Найдите круговую частоту w колебаний стержня, если в положении равновесия он расположен вертикально (см. рис.). Массами стержня, пружины, а также силами трения пренебречь. (2004 - 2006)

22. Груз массы m подвешен на пружине жесткости k. С помощью горизонтальной подставки груз удерживается в положении, когда пружина недеформирована. Затем подставку начинают опускать вниз с ускорением a (a < g).

Пренебрегая массой пружины, определите амплитуду колебаний груза, возникших после того, как груз оторвался от подставки. (2006)

23. Альфа-частица (ядро ) движется прямолинейно вдоль оси x под действием электрического поля с напряженностью , где и b - известные постоянные. В начальный момент времени альфа-частица покоилась в точке . Чему равна максимальная кинетическая энергия альфа-частицы в таком движении? Через сколько времени от начала движения достигается это максимальное значение кинетической энергии? (2006)

24. Положительно заряженная частица, двигаясь в плоскости (xy) с некоторой скоростью под углом α к оси x влетает в область (x > 0), где создано электрическое поле, вектор напряженности которого задан координатами , (β – положительная постоянная). Частица проникает на глубину L вдоль оси x, после чего спустя время t она вылетает обратно в область в область (x < 0). Найдите скорость движения частицы в области (x < 0). Излучением пренебречь. (2013)

25. На горизонтальной плоскости лежит брусок массы m, соединенный горизонтальной недеформированной невесомой пружиной жесткости k с вертикальной стенкой. Брусок сместили так, что пружина растянулась на x ₀, а затем отпустили. Определите коэффициент

трения между бруском и поверхностью, если известно число колебаний N, которое совершил брусок до остановки. (2013)

---

Дата добавления: 2015-07-11