
Читайте также:
|
9.1. Трактриса  задана отображением
задана отображением  :
:

 ,
,
где 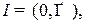
 - трехмерное евклидово пространство.
- трехмерное евклидово пространство.
Определить класс гладкости  . Является ли трактриса плоской кривой?
. Является ли трактриса плоской кривой?
9.2. Для плоских кривых

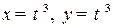
проверить эквивалентность при  и при
и при  .
.
9.3. Кривая на плоскости задана одним из трех способов: параметрически, в виде графика функции или неявно. Задать ее другими оставшимися способами. Выяснить расположение кривой на плоскости и нарисовать ее.
а)  при
при  ;
;
б)  при
при  ;
;
в)  при
при  ;
;
г)  при
при  ;
;
д)  ;
;
е) 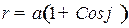 ,
,  (кардиоида);
(кардиоида);
ж) 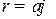 ,
,  (спираль Архимеда);
(спираль Архимеда);
з) 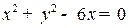 .
.
9.4. Показать, что кривая  ,
,
лежит на сфере.
9.5. Циклоидой называется плоская линия, которую описывает точка А окружности, катящейся без скольжения в плоскости (xOy) по неподвижной прямой (оси Ox). Написать параметрические уравнения циклоиды.
9.6. Кривая на плоскости задана одним из трех способов: параметрически, в виде графика функции или неявно. Написать уравнения касательной и нормали в данной точке.
а)  при
при 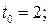

б)  при
при  ;
;
в)  при
при 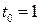 ;
;
г)  при
при  ,
,  ;
;
д)  ;
;
е) кривые 2 порядка на плоскости, заданные каноническими уравнениями;
ж)  при
при 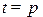 (циклоида);
(циклоида);
з)  (декартов лист);
(декартов лист);
и) 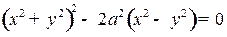 (лемниската Бернулли);
(лемниската Бернулли);
к)  ;
;
л) элементарные функции от одной переменной в произвольной точке из области определения.
Замечание. В пунктах з)-к) точки на кривых подберите самостоятельно.
9.7. В каких точках касательная к параболе 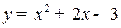 перпендикулярна прямой
перпендикулярна прямой  ; параллельна этой прямой?
; параллельна этой прямой?
9.8. Найти угол между кривыми в точке их пересечения
а) 
б)  .
.
9.9. Найти длины кривых из задачи 9.6 а) - ж), л) от  до
до  .
.
9.10. Найти кривизны кривых из задачи 9.6 а)-е), к) в указанных точках. Можно ли для данных кривых указать точки, в которых кривизна достигает своего максимального и минимального значений?
9.11. Напишите уравнение касательной прямой и нормальной плоскости, бинормали, главной нормали, соприкасающейся и спрямляющей плоскостей кривой  , заданной параметрически в трехмерном пространстве, в указанной точке. Определите класс гладкости кривой.
, заданной параметрически в трехмерном пространстве, в указанной точке. Определите класс гладкости кривой.
а) 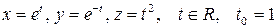 ;
;
б) 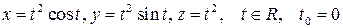 ;
;
в)  ;
;
г)  ,
, 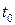 - любая точка кривой;
- любая точка кривой;
д)  ,
, 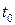 - любая точка кривой;
- любая точка кривой;
е) 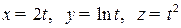 ,
, 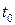 - любая точка кривой.
- любая точка кривой.
ж)
9.12. Написать уравнение касательной прямой и нормальной плоскости, бинормали, главной нормали, соприкасающейся и спрямляющей плоскостей кривой  , заданной как пересечение двух неявно заданных поверхностей, в точке
, заданной как пересечение двух неявно заданных поверхностей, в точке  :
:
а) 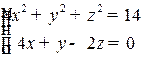 ,
,  ;
;
б) 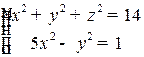 ,
,  .
.
9.13. Найти длины кривых из задачи 9.11 от 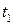 до
до  . Значения
. Значения 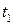 и
и  подберите сами.
подберите сами.
9.14 из задачи 9.11 при  . Значения
. Значения 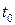 подберите сами.
подберите сами.
9.15.Н айти кривизну и кручение кривой 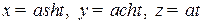 , где
, где  в ее произвольной точке.
в ее произвольной точке.
9.16. Найти координатные векторы канонического репера кривых из задачи 9.11 в указанных точках.
Дата добавления: 2015-07-11; просмотров: 60 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи по доказыванию | | | Сумма элементов |