Дополнительные задачи по теме

Использование одномерных массивов

Цель задания:

1. Изучение применения различных видов циклов при решении задач с использованием одномерных массивов.

2. Приобретение опыта решения задач с использованием одномерных массивов.

Содержание отчета:

1. Титульный лист оформленный в соответствии с ПРОЛОЖЕНИЕМ №1

2. В отчет включаются все задачи данного варианта задания.

3. Для каждого задания указывается:

a. Постановка задачи.

b. Текст программы.

c. Результаты отладки на тестах.

d. Анализ допущенных ошибок.

Методические указания

1. Программа должна правильно выполняться при любых значениях начальных данных.

2. При выводе ответа необходимо включить начальные значения.

3. Отчет высылается преподавателю на почту [e-mail] в теме письма указывается: Фамилия, группа номер работы (письма без указания темы не рассматриваются). Формат отчета.doc, или.docx. В течение трех рабочих дней вы получаете ответ по отчету. Результаты сдачи фиксируются преподавателем в файле «Сдачи работ.xlsx» размещенному в сети колледжа.

Теоретические вопросы

1.?

Варианты задания:

Вариант № 1

Вариант № 2

Вариант № 3

Вариант № 4

Вариант № 5

Вариант № 6

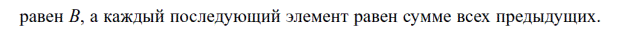
Вариант № 7

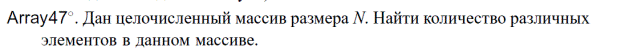
Вариант № 8

Вариант № 9

2 Даны целые числа a ₁,..., a_n (в этой последовательности могут быть повторяющиеся члены).Получить все числа, которые входят в последовательность по одному разу.

Вариант № 10

2 Даны целые числа a ₁,..., a_n (в этой последовательности могут быть повторяющиеся члены). Найти число различных членов последовательности.

Вариант № 11

2 Даны целые числа a ₁,..., a_n (в этой последовательности могут быть повторяющиеся члены). Выяснить, сколько чисел входит в последовательность по одному разу.

Вариант № 12

2. Даны целые числа a ₁,..., a_n (в этой последовательности могут быть повторяющиеся члены). Выяснить, имеется ли в последовательности хотя бы одна пара совпадающих чисел.

Вариант № 13

2. Даны целые числа m, a ₁,..., a ₂₀. Найти три натуральных числа i, j, k, каждое из которых не превосходит двадцати, такие, что a_i + a_j + a_k = m. Если таких чисел нет, то сообщить об этом

Вариант № 14

2. Даны пять различных целых чисел. Найти среди них два числа, модуль разности которых имеет:

а) наибольшее значение;

б) наименьшее значение.

Вариант № 15

2. Даны действительные числа x, y ₁,..., y ₂₅. В последовательности y ₁,..., y ₂₅ найти два члена, среднее арифметическое которых ближе всего к x.

Вариант № 16

2. Даны действительные числа x ₁,..., x ₁₇. Найти сумму значений .

Вариант № 17

2. Даны целые числа a ₁,..., a ₃₀. Пусть М - наибольшее, а m - наименьшее из a ₁,..., a ₃₀. Получить в порядке возрастания все целые из интервала (м, М), которые не входят в последовательность a ₁,..., a ₃₀.

Вариант № 18

2. Даны целые числа a ₁,..., a_n, b ₁,..., b_n. Верно ли, что эти две последовательности отличаются не более чем порядком следования членов?

Вариант № 19

2. Даны натуральные числа k, n, действительные числа a ₁,..., a_kn. Получить последовательности:

а) , ,..., ;

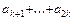Вариант № 20

2. Даны натуральные числа k, n, действительные числа a ₁,..., a_kn. Получить последовательности:

б) , ,..., ;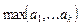

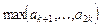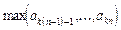Вариант № 21

2. Даны натуральные числа k, n, действительные числа a ₁,..., a_kn. Получить последовательности:

в) , ,..., ;

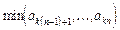Вариант № 22

2. Даны натуральные числа а ₁, а ₂ ,..., а_mn. Вычислить а ₁ а ₂ ... а_m+а_m+1а_{m+ 2} ... а _{2 m} +а _{(n- 1) m+ 1} а _{(n- 1) m+ 2} ... а_nm.

Вариант № 23

2. Даны натуральное число n, целые числа a ₁,..., a ₂₅, b ₁,..., b_n. Среди a ₁,..., a ₂₅ нет повторяющихся чисел, нет их и среди B[1],...,B[N].

а) Построить пересечение последовательностей a ₁,..., a ₂₅ и b ₁,..., b_n (т.е. получить в каком-нибудь порядке все числа, принадлежащие последовательности a ₁,..., a ₂₅ и последовательности b ₁,..., b_n одновременно).

Вариант № 24

2. Даны натуральное число n, целые числа a ₁,..., a ₂₅, b ₁,..., b_n. Среди a ₁,..., a ₂₅ нет повторяющихся чисел, нет их и среди B[1],...,B[N].

б) Построить объединение данных последовательностей.

Вариант № 25

2. Даны натуральное число n, целые числа a ₁,..., a ₂₅, b ₁,..., b_n. Среди a ₁,..., a ₂₅ нет повторяющихся чисел, нет их и среди B[1],...,B[N].

в) Получить все члены последовательности b ₁,..., b_n, которые не входят в последовательность a ₁,..., a ₂₅.

Вариант № 26

2. Даны натуральное число n, целые числа a ₁,..., a ₂₅, b ₁,..., b_n. Среди a ₁,..., a ₂₅ нет повторяющихся чисел, нет их и среди B[1],...,B[N].

г) Верно ли, что все члены последовательности a ₁,..., a ₂₅ входят в последовательность b ₁,..., b_n?

Вариант № 27

2. Даны натуральное число n, целые числа a ₁,..., a ₂₅, b ₁,..., b_n. Среди a ₁,..., a ₂₅ нет повторяющихся чисел, нет их и среди B[1],...,B[N].

д) Верно ли, что все члены последовательности b ₁,..., b_n входят в последовательность a ₁,..., a ₂₅?

Вариант № 28

2. Даны натуральное число n, целые числа a ₁,..., a ₂₅, b ₁,..., b_n. Среди a ₁,..., a ₂₅ нет повторяющихся чисел, нет их и среди B[1],...,B[N].

e) Верно ли, что все члены последовательности a ₁,..., a ₂₅ входят в последовательность b ₁,..., b_n и при этом a ₁ встречается в последовательности b ₁,..., b_n не позднее, чем a ₂, a ₂ - не позднее, чем a ₃, и т. д.?

Вариант № 29

Вариант № 30

Вариант № 31

Вариант № 32

Вариант № 33

Дополнительные задачи по теме

Дата добавления: 2015-07-11