Домашнее задание по дисциплине

«Математические основы автоматики и управления»

В качестве примера используется вариант 40.

Решение Задания 1.1.

С использованиемданных для варианта 40 структурная схема разомкнутой системы может быть представлена в таком виде:

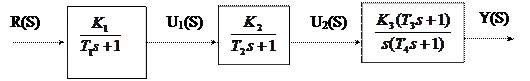Здесь K₁=2, K₂=8, K₃=12, T₁=2, T₂=3.5, T₃=0.2, T₄=0.5

Для решения поставленных задач сначала требуется определить передаточную функцию разомкнутой системы:

W(S)=G₁(S)G₂(S)G₃(S)= = .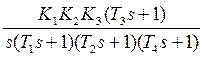

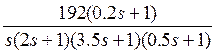На основе W(S) можно получить комплексную передаточную функцию W(jω) путем подстановки в W(S) величины s = jω, где ω-круговая частота.

W(jω)= ,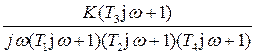

где К=К₁К₂К₃=192- коэффициент передачи разомкнутой системы.

Передаточная функция W(jω) является функцией комплексного переменного, поэтому может быть представлена в следующем виде:

W(jω)=А(ω)e^jφ(ω) = U(ω)+ jV(ω),

где А(ω)-амплитудная частотная характеристика(АХЧ), φ(ω)-фазовая частотная характеристика (ФХЧ), U(ω)-вещественная частотная характеристика (ВЧХ), V(ω) – мнимая частотная характеристика (МЧХ).

АЧХ – это по существу модуль W(jω), поэтому имеем

А(ω)= =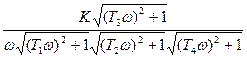

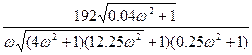
ФХЧ – определяется как алгебраическая сумма арктангенсов фаз комплексных операторов числителя и знаменателя W(jω), при этом фазы операторов числителя берутся положительными, а знаменателя – отрицательными. Отсюда

φ(ω)=arctg 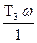- arctg 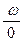- arctg 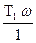- arctg 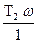- arctg =

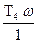= arctg 0.2 ω- 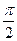- arctg 2 ω - arctg 3.5 ω - arctg 0.5 ω

Для получения ВХЧ и МХЧ сначала необходимо умножить W(jω) на сопряженные операторы знаменателя, а затем выделить U(ω) и V(ω), а именно:

W(jω) = =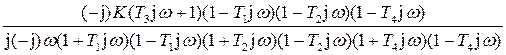

= =

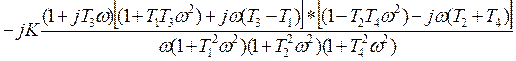=-jК =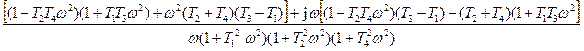

Отсюда

U(ω) = ,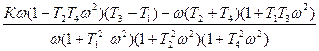

V(ω) = .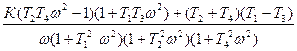

Решение задания 1-2.

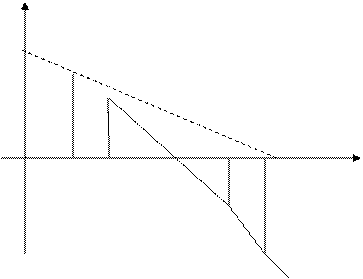
Для построения ЛАЧХ используется логарифмическая сетка с координатами L(ω) = 20 lg A(ω) и lg ω.

Сначала на оси частот откладываются точки сопряжения (изломы) ЛАЧХ ω_i= 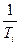. Отложим эти частоты с учетом значений постоянных времени Т_i (без точного расчета lg ω_i):

Т₂ > Т₁ > Т₄ > Т₃,

.

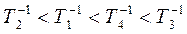Затем проводим низкочастотный участок L(ω)= 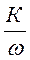Он согласно теории имеет отрицательный наклон -20 децибел на декаду и проходит через точку ω=К. В точке ω₂= 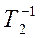ЛАЧХ претерпевает излом -20 дБ/дек, т.к. оператор (Т₂ j +1) находится в знаменателе ПФ. В итоге наклон будет равен

-40 дБ/дек. На частотах ω₁ = 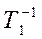и ω₄ = 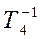ЛАЧХ также претерпевает изломы по -20 дБ/дек, а в точке ω₃ = 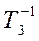излом L(ω) на +20 дБ/дек, т.к. оператор (Т₃ j +1) находится в числителе W(s).

T₃^-1

T₄^-1

T₂^-1

T₁^-1

	-80
		-60

_-60

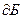
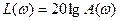
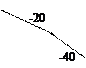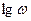
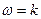
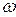
Решение задания 1.3.

Построение годографа W(jω) осуществляется в координатах V(ω) и U(ω).

Для оценки устойчивости достаточно осуществить расчеты V(ω) и U(ω) в области точки (-1, j0).

а) б)

	-1

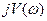
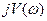
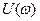
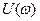
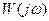
Если годограф W(jω) не охватывает точку (-1, j0), то замкнутая система устойчивая (рис.а), если охватывает – то не устойчивая (рис.б).

Примечание: Для удобства построения годографа W(jω) целесообразно представить зависимость V(ω)= f (U(ω)) в табличном виде:

ω
V(ω)
U(ω)

Выполнение задания 2.1.

В соответствии с заданными состояниями ключей (К1, К3 – замкнуты, остальные разомкнуты) получим следующую схему

e

y  

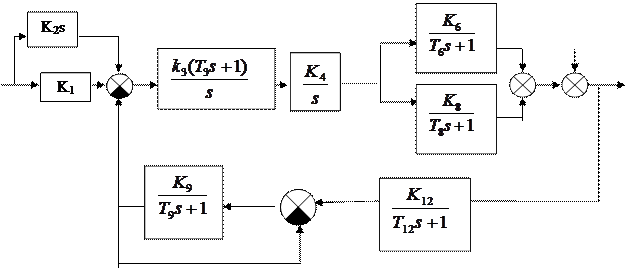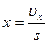
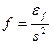
Рис. Структурная схема САУ

Выполнение задания 2.2

Для получения передаточной функции замкнутой системы Ф(S) сначала целесообразно преобразовать структурную схему, заменив типовые соединения (параллельное, последовательное, встречно-параллельное) одним звеном. В итоге получим:

W₆₈

e

W₃₄

W₂₁

		y
	W90
		W12

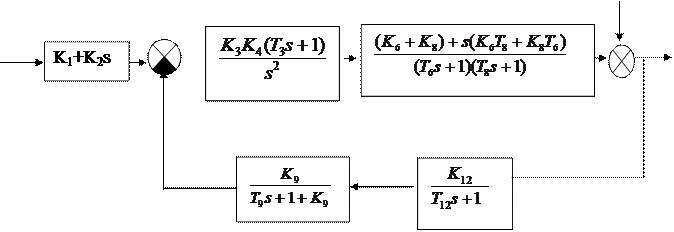
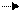
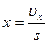
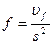
W₂₁(S) = W₂(S)+W₁(S) = K₂S+K₁)

W₃₄(S) = W₃(S)W₄(S) =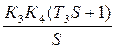

W₆₈(S) = W₆(S)W₈(S) = + =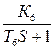

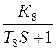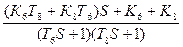
W₉₀(S) = = =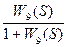

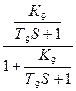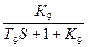
Далее получим Ф(S) = 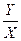по следующему правилу: знаменатель равен 1+произведение ПФ всех звеньев замкнутого контура, числитель равен произведению ПФ всех звеньев, лежащих на пути от X к выходу Y.

Ф(S) = = =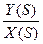

=

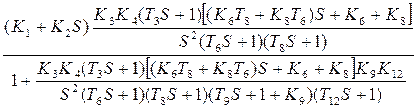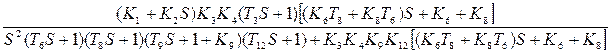
Решение задания 2.3.

Ошибка в установившимся режиме определяется по выражению

e_уст= 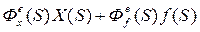, при S=0.

Таким образом для оценки ошибки требуется определить две передаточные функции: 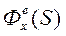ПФ для ошибки е по входному воздействию X, 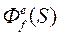ПФ для ошибки e по возмущению f.

=

=

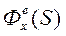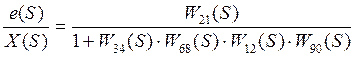
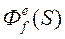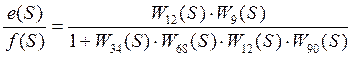
После подстановки W_i(S) и дальнейших преобразований (как для Ф(S)) получатся искомые 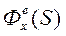и 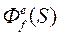. Затем необходимо подставить в ПФ значения 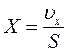и 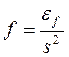, осуществить возможные сокращения и затем положить S=0. В итоге получится искомое значение e_уст.

Дата добавления: 2015-07-11